为实习准备的数据化结构(8)-- 倾心图解红黑树
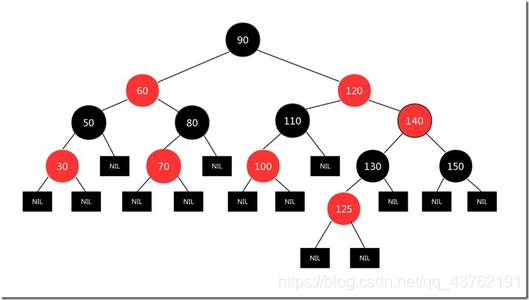
红黑树
红黑树(Red Black Tree) 是一种自平衡二叉查找树,是在计算机科学中用到的一种数据结构。
红黑树是一种平衡二叉查找树的变体,它的左右子树高差有可能大于 1,所以红黑树不是严格意义上的平衡二叉树(AVL),但 对之进行平衡的代价较低, 其平均统计性能要强于 AVL 。
由于每一棵红黑树都是一颗二叉排序树,因此,在对红黑树进行查找时,可以采用运用于普通二叉排序树上的查找算法,在查找过程中不需要颜色信息。
红黑树的特征
红黑树是每个结点都带有颜色属性的二叉查找树,颜色或红色或黑色。在二叉查找树强制一般要求以外,对于任何有效的红黑树我们增加了如下的额外要求:
性质1. 结点是红色或黑色。
性质2. 根结点是黑色。
性质3. 所有叶子都是黑色。(叶子是NULL结点)(这个性质我也不知道有什么用,最好配上上面的图看,不然会晕)
性质4. 每个红色结点的两个子结点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色结点)
性质5. 从任一节结点到每个叶子的所有路径都包含相同数目的黑色结点
- 1
- 2
- 3
- 4
- 5
这些约束强制了红黑树的关键性质: 从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。这个在高度上的理论上限允许红黑树在最坏情况下都是高效的。
是性质4导致路径上不能有两个连续的红色结点确保了这个结果。最短的可能路径都是黑色结点,最长的可能路径有交替的红色和黑色结点。因为根据性质5所有最长的路径都有相同数目的黑色结点,这就表明了没有路径能多于任何其他路径的两倍长。
红黑树自平衡的奥秘
红黑树能够实现自平衡,靠的是三个法宝:左旋、右旋和变色。
对于旋转我就不再多说了,前面的AVL树要是不够看可以再看看伸展树。
左旋:以某个结点作为支点(旋转结点),其右子结点变为旋转结点的父结点,右子结点的左子结点变为旋转结点的右子结点,左子结点保持不变。
右旋:以某个结点作为支点(旋转结点),其左子结点变为旋转结点的父结点,左子结点的右子结点变为旋转结点的左子结点,右子结点保持不变。
变色:结点的颜色由红变黑或由黑变红。
- 1
- 2
- 3
红黑树的查找也不说了,它是二叉树,所以二叉树怎么查找,红黑树就怎么查找。
红黑树自平衡操作
插入节点
第一步: 将红黑树当作一颗二叉查找树,将节点插入。
第二步:将插入的节点着色为"红色"。为什么是红色?你猜啊
(看一下性质五)
第三步: 通过一系列的旋转或着色等操作,使之重新成为一颗红黑树。
第二步中,将插入节点着色为"红色"之后,不会违背"特性(5)"。那它到底会违背哪些特性呢?
很显然,只有性质4.(每个红色结点的两个子结点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色结点))比较危险。
那接下来,想办法使之"满足性质4. ",就可以将树重新构造成红黑树了。
昨天我躺在床上,辗转反侧,梦中顿悟,红黑树插入会有以下这么几种情况:
1、被插入的节点是根节点。
那最好办,那说明是空树,直接涂黑就好。
2、新插入节点的父节点是黑的(新插入的节点,不会有子节点存在,这个可以放心)
这个更好办,就插入就完了
3、新插入节点的父节点是红的
那就有意思了。具体情况下面讨论
- 1
- 2
- 3
- 4
- 5
- 6
对于上面第三种情况的再分析:
1、新节点的父节点的兄弟节点是红的
//以下两种情况默认包含了父节点没有兄弟的情况
2、新节点的父节点的兄弟节点是黑的,且当前节点是其父节点的 右 孩子
3、新节点的父节点的兄弟节点是黑的,且当前节点是其父节点的 左 孩子
(为什么要这样分?不急慢慢看,我也纳闷儿呢!!!)
上面三种情况处理问题的核心思路都是:将红色的节点移到根节点;然后,将根节点设为黑色。下面对它们详细进行介绍。
- 1
- 2
- 3
- 4
- 5
- 6
- 7
情况一:
策略:
(01) 将“父节点”设为黑色。
(02) 将“叔叔节点”设为黑色。
(03) 将“祖父节点”设为“红色”。
(04) 将“祖父节点”设为“当前节点”(红色节点);即,之后继续对“当前节点”进行操作。
- 1
- 2
- 3
- 4
这里需要说明一下,当祖父节点被染红,它可能会和它自己的父节点起冲突,所以需要向上递归。
就碧如这样:
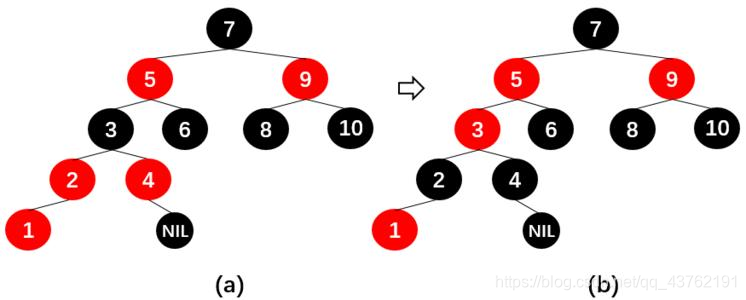
为什么采用这个策略?
“当前节点”和“父节点”都是红色,违背“性质4. ”。所以,将“父节点”设置“黑色”以解决这个问题。
但是,将“父节点”由“红色”变成“黑色”之后,违背了“性质5. ”:因为,包含“父节点”的分支的黑色节点的总数增加了1。
解决这个问题的办法是:将“祖父节点”由“黑色”变成红色,同时,将“叔叔节点”由“红色”变成“黑色”。
这里为什么要将“叔叔节点”也变黑?思考思考,不难理解的。
理解不了的话对着上面那张图去数性质5.
这里需要再说明一下,当祖父节点被染红,它可能会和它自己的父节点起冲突,所以需要向上递归。
情况二:
策略:
(01) 将“父节点”作为“新的当前节点”。
(02) 以“新的当前节点”为支点进行左旋。
- 1
- 2
草率了。。。
哎,看图吧:
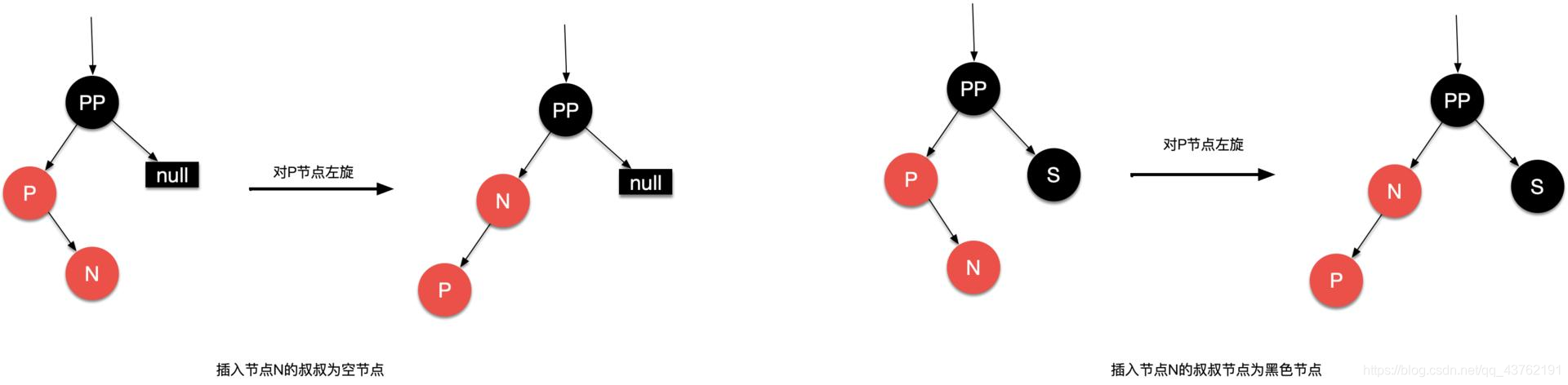
呐,弄完之后,变成了第三种情况了。
情况三:
策略:
(01) 将“父节点”设为“黑色”。
(02) 将“祖父节点”设为“红色”。
(03) 以“祖父节点”为支点进行右旋。
- 1
- 2
- 3
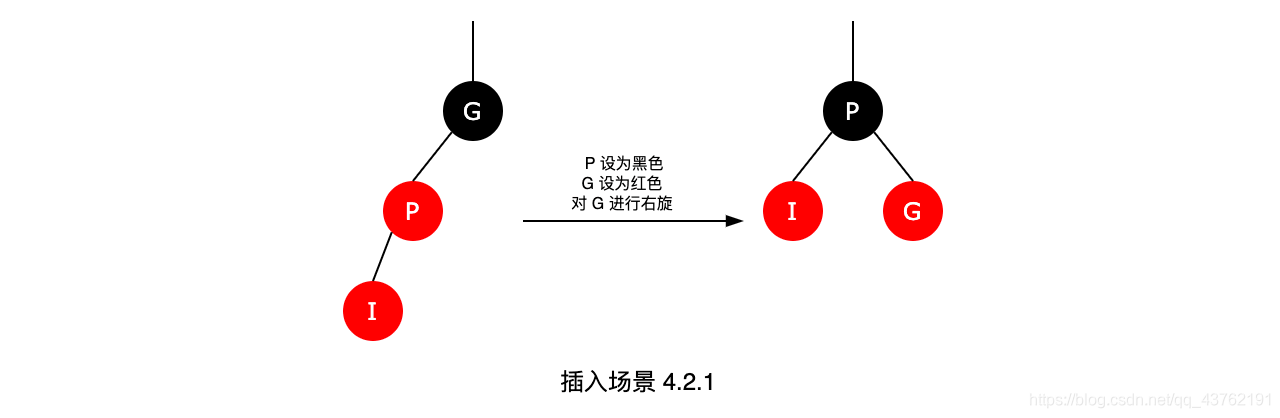
为什么采用这个策略?
为了便于说明,我们设置“当前节点”为S(Original Son),“兄弟节点”为B(Brother),“叔叔节点”为U(Uncle),“父节点”为F(Father),祖父节点为G(Grand-Father)。
S和F都是红色,违背了红黑树的“性质4. ”,我们可以将F由“红色”变为“黑色”,就解决了“违背‘性质4. ’”的问题;但却引起了其它问题:违背“性质5. ”,因为将F由红色改为黑色之后,所有经过F的分支的黑色节点的个数增加了1。那我们如何解决“所有经过F的分支的黑色节点的个数增加了1”的问题呢? 我们可以通过“将G由黑色变成红色”,同时“以G为支点进行右旋”来解决。
对于红黑树的节点插入,我讲明白了吗?
关注点赞收藏,我们继续往下。
删除节点
相较于插入操作,红黑树的删除操作则要更为复杂一些。删除操作首先要确定待删除节点有几个孩子,如果有两个孩子,不能直接删除该节点。而是要先找到该节点的前驱(该节点左子树中最大的节点)或者后继(该节点右子树中最小的节点),然后将前驱或者后继的值复制到要删除的节点中,最后再将前驱或后继删除。
第一步:将红黑树当作一颗二叉查找树,将节点删除。
第二步:通过"旋转和重新着色"等一系列来修正该树,使之重新成为一棵红黑树。
在第一步中"将红黑树当作一颗二叉查找树,将节点删除"后,可能违反"性质(2)、(4)、(5)"三个性质。第二步需要解决上面的三个问题,进而保持红黑树的全部特性。
删除一个红色节点,并不会有什么不适。
所以我们将目光聚焦在删除一个黑色节点上。
删除一个节点有以下四种情况:
1.删除的节点没有孩子
2.删除的节点只有左子树
3.删除的节点只有右子树
*4.删除的节点拥有左子树和右子树
- 1
- 2
- 3
- 4
其实只有上面前三种情况,对于第四种情况,可以找到待删除节点的直接后继节点,用这个节点的值替代待删除节点,接着情况转变为删除这个直接后继节点,情况也变为前三种之一。(前驱和后继至多只有一个孩子节点)
1.删除的节点只有左子树或只有右子树:

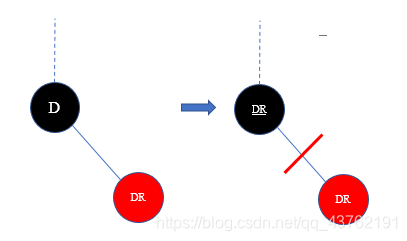
2.删除的节点没有孩子
1)待删除节点是红色的,直接删去这个节点。
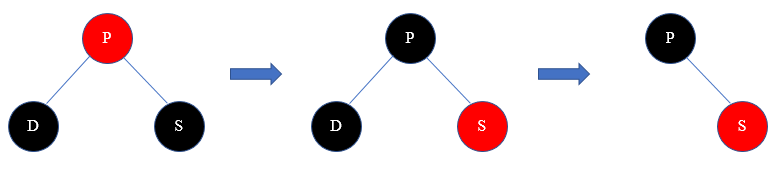
2)父节点P是红色节点
解决方案:把P节点染成黑色,兄弟节点染成红色,删除节点D。
- 1
- 2
- 3
3)兄弟节点S是红色节点
- 1
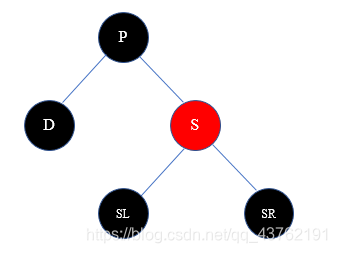
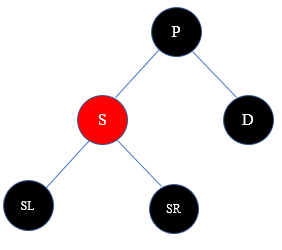
解决方案:把P染成红色,S染成黑色,然后以P为轴做相应的旋转操作(D为P的左子树则左旋,否则右旋)
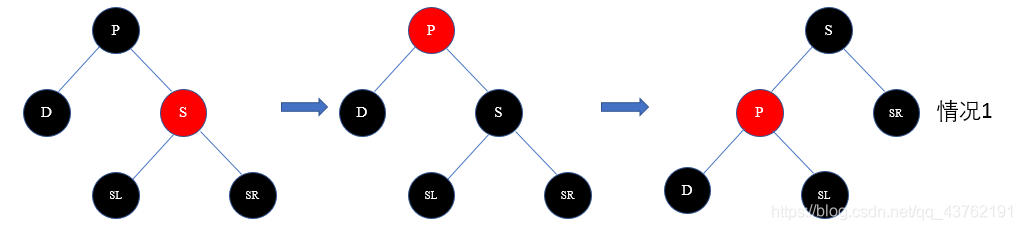
4)节点D的远亲侄子为红色节点的情况(父节点P可红可黑)
- 1
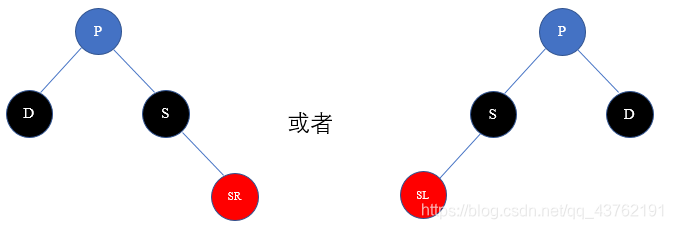
解决方案:交换P和S的颜色,然后把远亲侄子节点SR/SL设置为黑色,再已P为轴做相应的旋转操作(D为P的左子树则左旋,否则右旋),删除节点D。

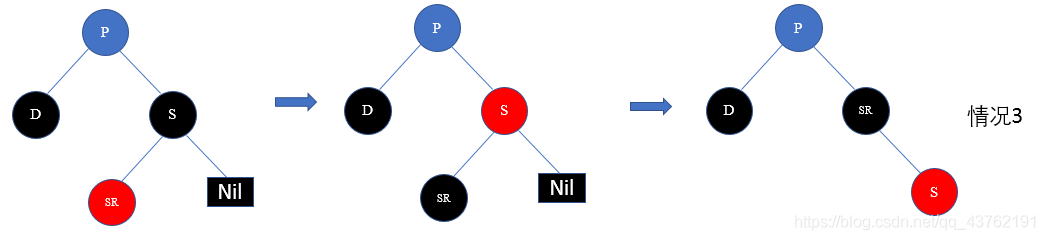
5)节点D的近亲侄子为红色节点的情况(父节点P可红可黑)
- 1

解决方案:把S染成红色,把近亲侄子节点SR/SL染成黑色,然后以节点S为轴做相应的旋转操作(D为P的左子树则右旋,否则左旋),变成了情况4,按照情况4进行操作。
6)节点D,P,S均为黑色节点
- 1

解决方案:把D删去,然后把节点S染成红色。
①从节点P往上依然是全黑的情况

②从节点P往上是其他情况

哇,累。

文章来源: blog.csdn.net,作者:看,未来,版权归原作者所有,如需转载,请联系作者。
原文链接:blog.csdn.net/qq_43762191/article/details/113789434
- 点赞
- 收藏
- 关注作者


评论(0)