LeetCode 45跳跃游戏&46全排列

原创公众号：bigsai，回复进群加入力扣打卡群。
昨日打卡：LeetCode 42字符串相乘&43通配符匹配

跳跃游戏

题目描述：

给定一个非负整数数组，你最初位于数组的第一个位置。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
你的目标是使用最少的跳跃次数到达数组的最后一个位置。

示例:

输入: [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
从下标为 0 跳到下标为 1 的位置，跳 1 步，然后跳 3 步到达数组的最后一个位置。
说明:
假设你总是可以到达数组的最后一个位置。

分析：

这题的话也是运用了不同的方法，从复杂到简单。

法一：枚举

枚举的思路很简单，二重循环，第一次循环遍历每个数，第二次循环遍历长度更新这个范围内能够更新到的最小跳数。如果能跳到该位置并且跳跃次数更少就更新。算法想法简单，初始需要将除第0位其他设置为非常大的值(以便有更小的值进行更新)

实现代码为：

 public  int jump(int[] nums) { int dp[]=new int[nums.length]; for(int i=1;i<nums.length;i++) { dp[i]=Integer.MAX_VALUE; } for(int i=0;i<nums.length;i++) { int time=dp[i]+1; for(int j=0;j<nums[i];j++) { if(j+i+1<nums.length) { if(dp[j+i+1]>time) dp[j+i+1]=time; } } } //System.out.println(Arrays.toString(dp)); return dp[nums.length-1];
}

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
 

不过效果很糟糕。

法二：bfs
在这条路行不通之后，就开始寻找另一条路。我便想着用优先队列搜素，具体比较麻烦详细可以看代码，主要讲第三种方法：

class node
{
	int time;
	int index;
	public node(int time,int index) {
		this.time=time;
		this.index=index;
	}
}
 public  int jump(int[] nums) { boolean jud[]=new boolean[nums.length];
	 Queue<node>q1=new PriorityQueue<node>(new Comparator<node>() { @Override public int compare(node o1, node o2) { if(o1.time==o2.time) { return o2.index-o1.index; } return o1.time-o2.time; }
	});
	 q1.add(new node(0, 0));
	 while (!q1.isEmpty()) {
		node team=q1.poll();
		int time=team.time+1;
		int index=team.index;
		for(int i=1;i<=nums[index];i++)//前进的位置
		{ if(index+i<nums.length&&!jud[index+i]) { if(index+i==nums.length-1)return time; q1.add(new node(time, index+i)); jud[index+i]=true; }
		}
	}
	 return 0;
 }

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
 

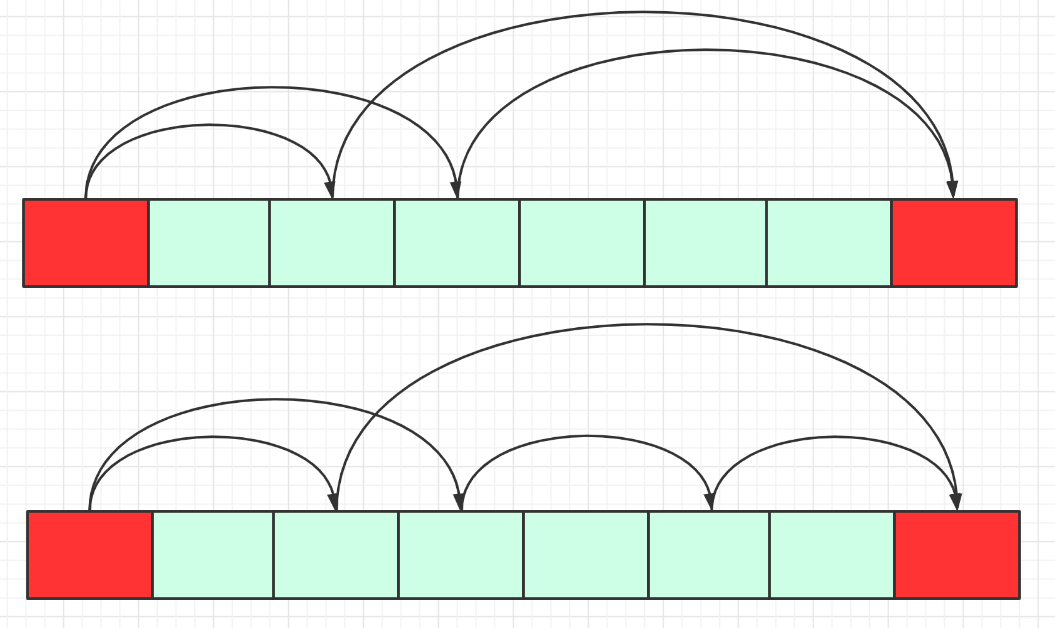
法三：贪心
当我以为9ms很快的时候，发现原来这个速度还是很慢，就想肯定有一种近O(n)的方法，在这里索性分享给大家。

我们在这里需要的实什么?

• 找到最少的跳跃次数到达最后

影响我们正常计算的最大障碍是什么？

• 重复计算、覆盖情况.无论是跳跃方式和跳跃次数到达终点都可能不止一种。

但是有一点非常重要的是：每个节点跳跃的时候是一个从他开始的覆盖区间范围，所以我们能否知道第一次跳多远。第二次跳多远呢？第三次呢？

很简单，所有的起始点是0号位置，也就是第一次一定是从0号跳到的一个区间节点。而第二次就是这个区间内能够跳到的最远距离都是2次，第三次就是除掉第二次节点后面能够跳到的区间……这样一直到能够覆盖到最后即可完成。

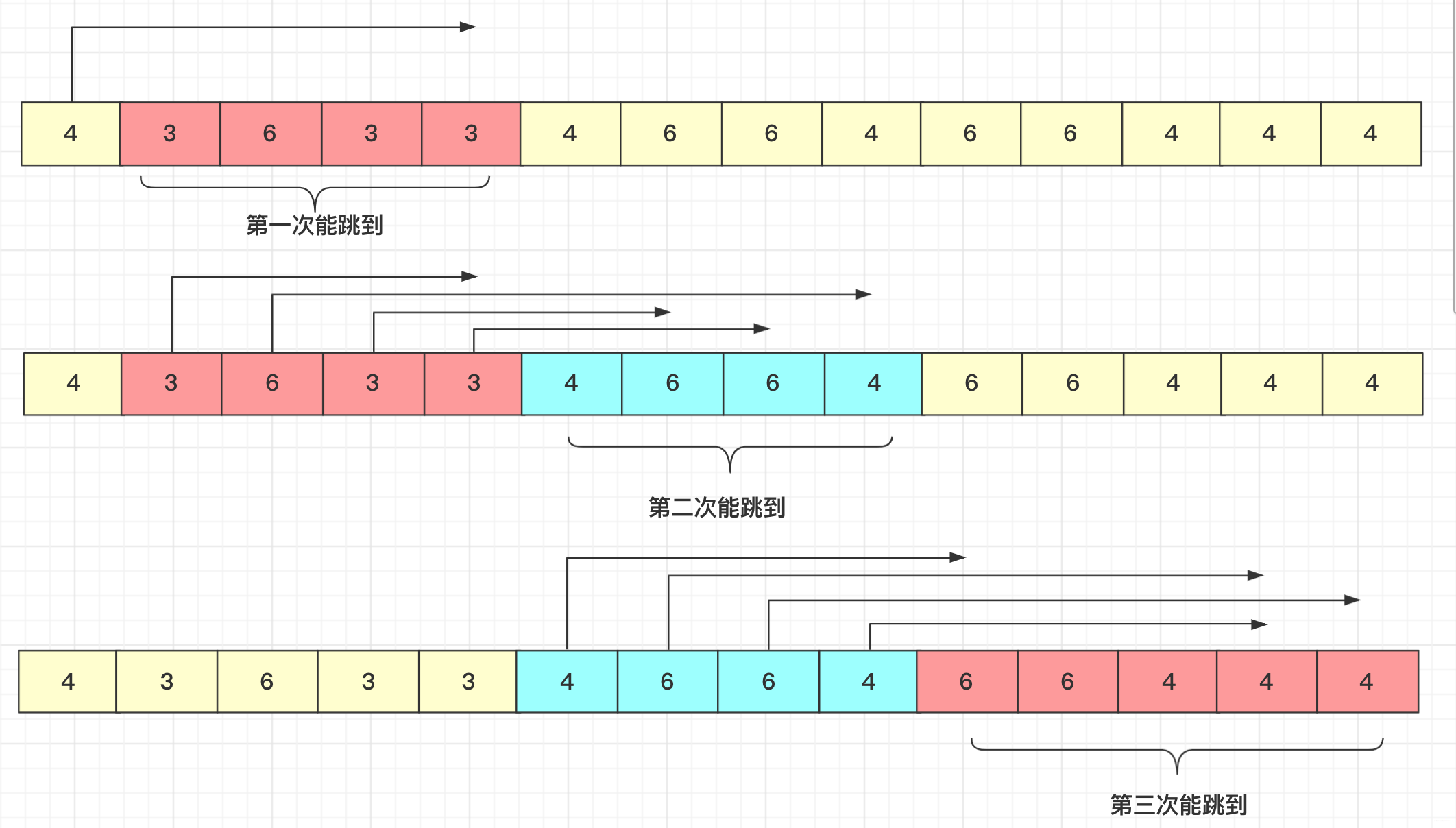
在具体实现的时候，记录当前的最大长度，用一个time[]数组表示到达当前节点需要的跳数，从前往后，如果最大长度大于当前的maxsize，就说明需要加一次更新，如果小于等于maxsize，对应位置则不需要更新。

实现代码为：

public  int jump(int[] nums) {
	int len=nums.length;
	int time[]=new int[len]; int maxsize=0;
	for(int i=0;i<len;i++)
	{
		if(i+nums[i]>maxsize)
		{ for(int j=maxsize+1;j<=i+nums[i];j++) { if(j<len) { time[j]=time[i]+1; maxsize=j; } else { break; } }
		}
	}
	return time[len-1];
}

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
 

还能优化成1ms的就留给你们来了！

全排列

全排列的两种实现方式这里就不累述，大家可以参考：全排列两种实现方式

实现方式为：

 public List<List<Integer>> permute(int[] nums) {
		List<List<Integer>>list=new ArrayList<List<Integer>>();
		arrange(nums,0,nums.length-1,list);
		return list;
	 }

	private void arrange(int[] nums, int start, int end, List<List<Integer>> list) { if(start==end) { List<Integer>list2=new ArrayList<Integer>(); for(int a:nums) { list2.add(a); } list.add(list2); } for(int i=start;i<=end;i++) { swap(nums,i,start); arrange(nums, start+1, end, list); swap(nums, i, start); } }

	private void swap(int[] nums, int i, int j) {
		int team=nums[i];
		nums[i]=nums[j];
		nums[j]=team;
	}

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
 

本次就到这里啦，感觉不错记得点赞或一键三连哦，个人公众号：bigsai 回复 bigsai 更多精彩和资源与你分享。

文章来源: bigsai.blog.csdn.net，作者：Big sai，版权归原作者所有，如需转载，请联系作者。

原文链接：bigsai.blog.csdn.net/article/details/109269947