前言

在有向图和无向图中，如果节点之间无权值或者权值相等，那么dfs和bfs时常出现在日常算法中。不仅如此，dfs，bfs不仅仅能够解决图论的问题，在其他问题的搜索上也是最基础(但是策略不同)的两种经典算法。

并且五大经典算法的回溯算法其实也是dfs的一种。dfs,bfs基础能够解决搜索类问题的大部分情况，只不过搜索随着数据增大而呈非线性的增长，所以两种算法在数据较多的情况是不太适用的。

邻接矩阵和邻接表

邻接矩阵：
邻接矩阵就是用数组(二维)表示图。具体可以看下面例子。当然，这种情况很容易造成空间浪费，所以很多人进行空间优化，甚至是邻接表的方式。

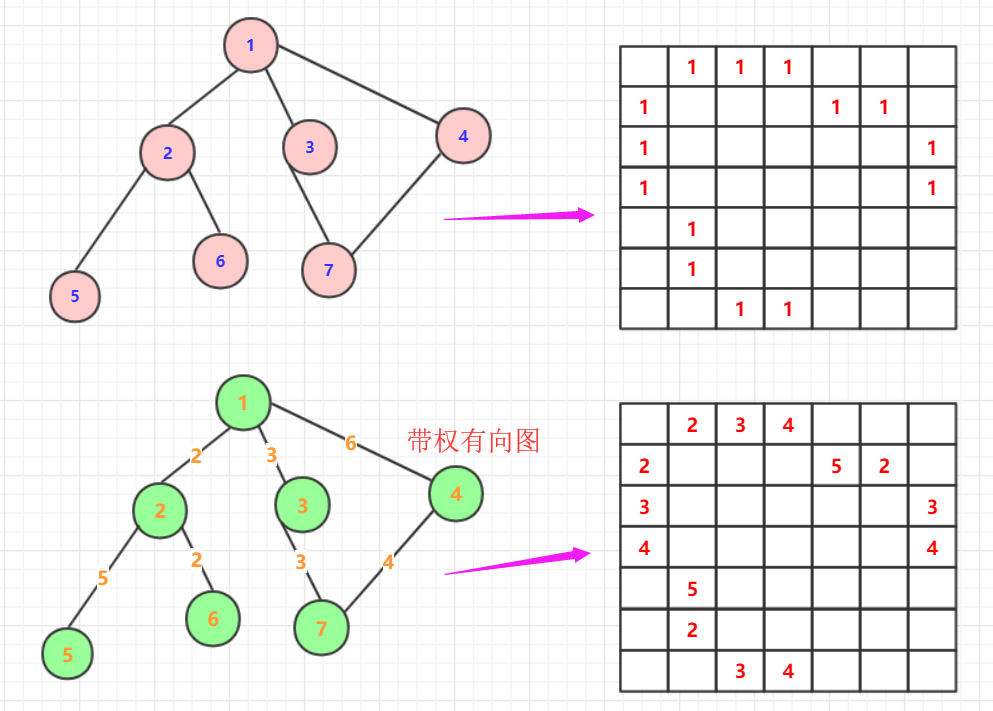
邻接表：
而邻接表则是数组套链表。这样可以比起邻接矩阵节省不少空间，但是如果无向图依然会重复浪费一半空间，就有十字链表，多重链接表等等出现。同时，对于有权图来说，只需对节点加一个属性weight即可！

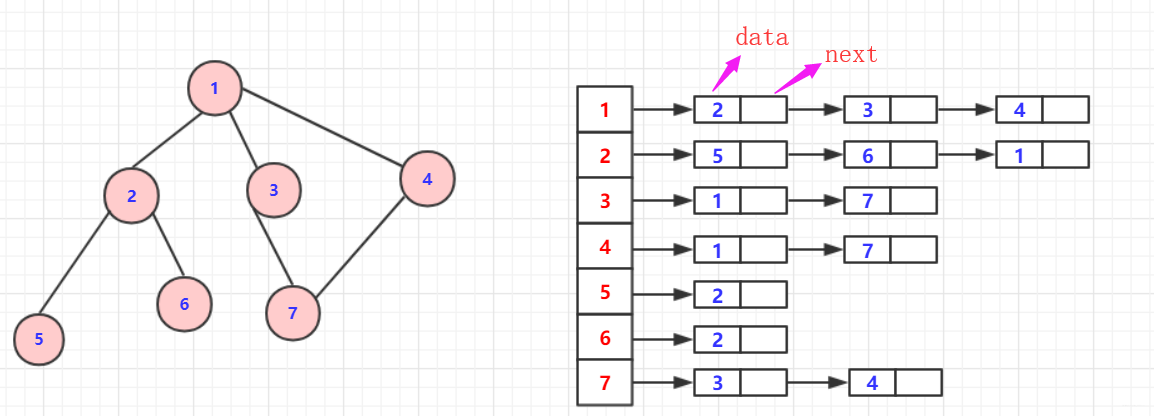
深度优先搜索(dfs)

概念：

深度优先搜索属于图算法的一种，英文缩写为DFS即Depth First Search.其过程简要来说是对每一个可能的分支路径深入到不能再深入为止，而且每个节点只能访问一次.

简单的说，要完成dfs要有前提条件.就是有联通点。单个节点dfs就断掉了，他要找打和它联系的节点。dfs入手可能比bfs简单的原因是dfs大部分之间利用递归的走向完成dfs，而很少需要标记。

我们通常使用邻接表(一维数组套链表a[List])或者邻接矩阵(二维数组a[][])储存图的信息。有时为了优化空间会选择十字链表或者邻接多重表进行存储节省空间，但是操作往往是很复杂的。并且一般来说图的更大需要设计算法的优化，所以这里例子使用邻接矩阵完成！

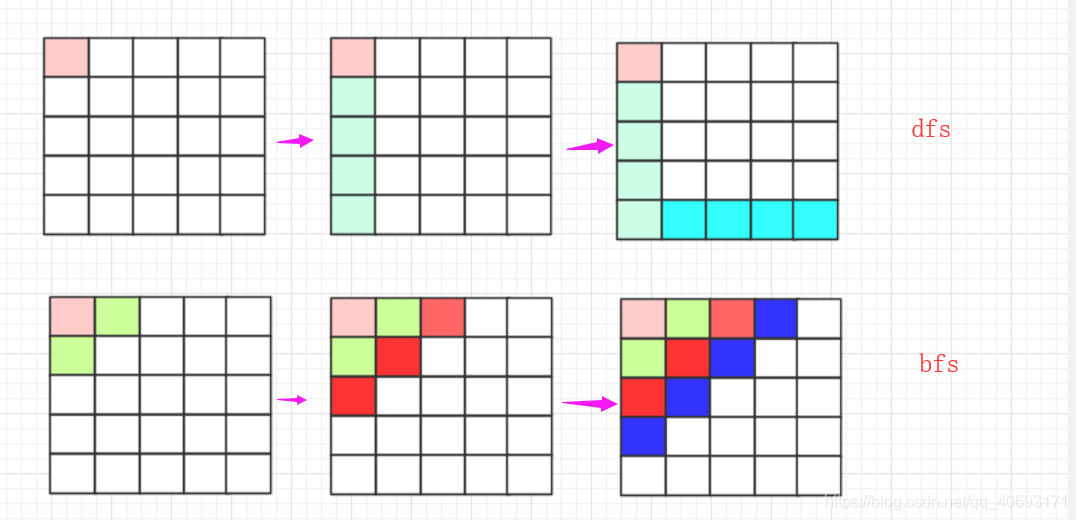
对于dfs的流程来说，大致可以认为是这样：

• 从初始点开始按照一个方向遍历，这个方向到尽头停止后到另一个方向，，，直到所有操作完成退出！
• 深度优先搜索执行过程像是一个栈的操作。喜新厌旧。总是处理最新加入的节点，这点递归恰好满足其性质，并且递归代码写起来也更简洁。
• dfs的流程可以参考二叉树的前序遍历，它实质就是一个dfs。

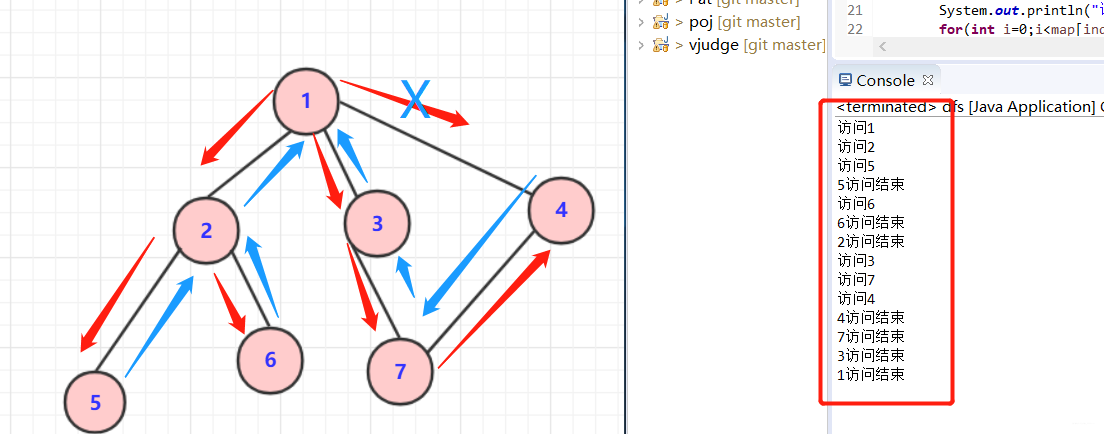
对于上图的dfs。可以用一下代码来表示：

package 图论;
public class dfs {
	static boolean isVisit[];
	public static void main(String[] args) {
		int map[][]=new int[7][7];
		isVisit=new boolean[7];
		map[0][1]=map[1][0]=1;
		map[0][2]=map[2][0]=1;
		map[0][3]=map[3][0]=1; map[1][4]=map[4][1]=1;
		map[1][5]=map[5][1]=1;
		map[2][6]=map[6][2]=1;
		map[3][6]=map[6][3]=1; isVisit[0]=true;
		dfs(0,map);//从0开始遍历
	}
	private static void dfs(int index,int map[][]) {
		// TODO Auto-generated method stub
		System.out.println("访问"+(index+1)+"  ");
		for(int i=0;i<map[index].length;i++)//查找联通节点
		{ if(map[index][i]>0&&isVisit[i]==false) { isVisit[i]=true; dfs(i,map); }
		}
		System.out.println((index+1)+"访问结束 ");
	}
}

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
 

大致顺序访问为

宽度(广度)优先搜索(bfs)

概念：

BFS，其英文全称是Breadth First Search。 BFS并不使用经验法则算法。从算法的观点，所有因为展开节点而得到的子节点都会被加进一个先进先出的队列中。一般的实验里，其邻居节点尚未被检验过的节点会被放置在一个被称为 open 的容器中（例如队列或是链表），而被检验过的节点则被放置在被称为 closed 的容器中。（open-closed表）

简单来说，bfs就是先进先出的队列遍历，然而这样在分布的情况就是按层遍历，可以参考二叉树遍历的层序遍历！

如果从路径上走来看，dfs就是一条跑的很快的疯狗，到处乱咬。没路了就转头，再没路了再跑回来去其他地方，而bfs就像是一团毒气，慢慢延申！

就拿上述的图来说，我们使用邻接表来实现遍历。

import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.List;
import java.util.Queue;

public class bfs {
	public static void main(String[] args) {
		List<Integer> map[]=new ArrayList[7];
		boolean isVisit[]=new boolean[7];
		for(int i=0;i<map.length;i++)//初始化
		{ map[i]=new ArrayList<Integer>();
		}
		map[0].add(1);map[0].add(2);map[0].add(3);
		map[1].add(0);map[1].add(4);map[1].add(5);
		map[2].add(0);map[2].add(6);
		map[3].add(0);map[3].add(6);
		map[4].add(1);
		map[5].add(1);
		map[6].add(2);map[6].add(3); Queue<Integer>q1=new ArrayDeque<Integer>();
		q1.add(0);isVisit[0]=true;
		while (!q1.isEmpty()) { int va=q1.poll(); System.out.println("访问"+(va+1)); for(int i=0;i<map[va].size();i++) { int index=map[va].get(i); if(!isVisit[index]) { q1.add(index); isVisit[index]=true; } }
		}
	}
}

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
 

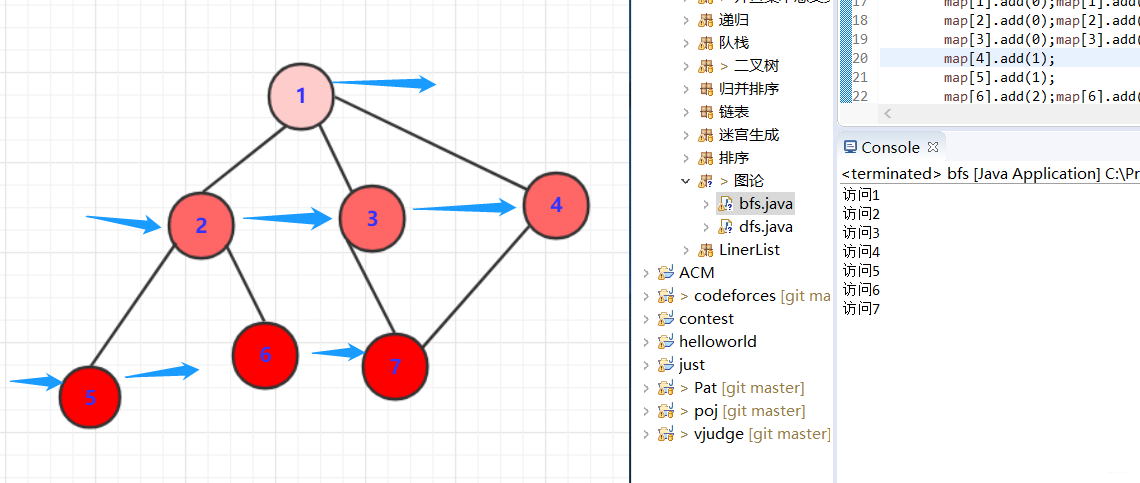
总结与比较

上面说到dfs和bfs往往是在寻路上的两个极端的表现！当然在不同场景使用可能也有些不同。

• dfs可以运用在查找和爬虫中，如果爬虫的话那么更多是优先找到不同链接，可用于统计等。而在查找中比如迷宫类可以利用dfs判断是否存在路径，出路等等。
• bfs也可以运用在算法和爬虫之中。而bfs优先处理自己周围的资源。所以在爬虫可以用于遍历网站，搜寻整个网站的价值信息等等，笔者以前用爬虫+bfs实现过下载网站的模板(17素材的网页模板)。而在算法中，在迷宫或者无权图中，bfs可以找到最短路径。
  

在上面可以看得出在邻接矩阵实现储存上浪费很多空间，但有些情况使用二维数组很合适——迷宫类问题。我们在面试学习，会经常遇到迷宫类需要bfs找最短路径，或者dfs查询是否存在。或者双bfs又或者dfs+bfs等等解决具体问题。

最后，希望大家能关注我(bigsai)，我们一起学习数据结构与算法！感觉还行，可以动动小手，点个赞！

文章来源: bigsai.blog.csdn.net，作者：Big sai，版权归原作者所有，如需转载，请联系作者。

原文链接：bigsai.blog.csdn.net/article/details/100185967