数据结构与算法—哈夫曼树详解与构造
【摘要】
文章目录
介绍哈夫曼树的构造代码实现:
介绍
定义:
给定N个权值作为N个叶子结点,构造一棵二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。
简而言之,就是按照一个贪心思想和规则进行树的构造,而构造出来的这个树的权值最小!
其中W...
介绍
定义:
- 给定N个权值作为N个叶子结点,构造一棵二叉树,若该树的带权路径长度达到最小,称这样的二叉树为
最优二叉树,也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。

简而言之,就是按照一个贪心思想和规则进行树的构造,而构造出来的这个树的权值最小!
其中WPL表示计算出的权值。至于为什么按照哈夫曼树方法构造得到的权重最小。这里不进行证明。对于哈夫曼树,他的每个非叶子节点都有两个孩子因为哈夫曼树的构造就是自底向上的构造,两两合并。
WPL计算方法:
WPL=求和(wi li)其中wi是第i个节点的权值(value)。li是第i个节点的长(深)度.
哈夫曼树的构造
初始时候各个数直都是一个单节点森林!然后进行排序。
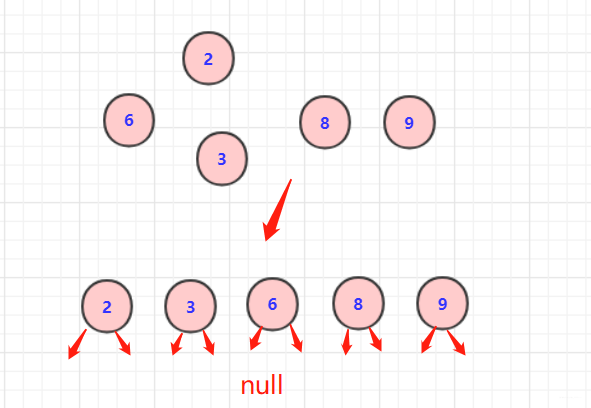
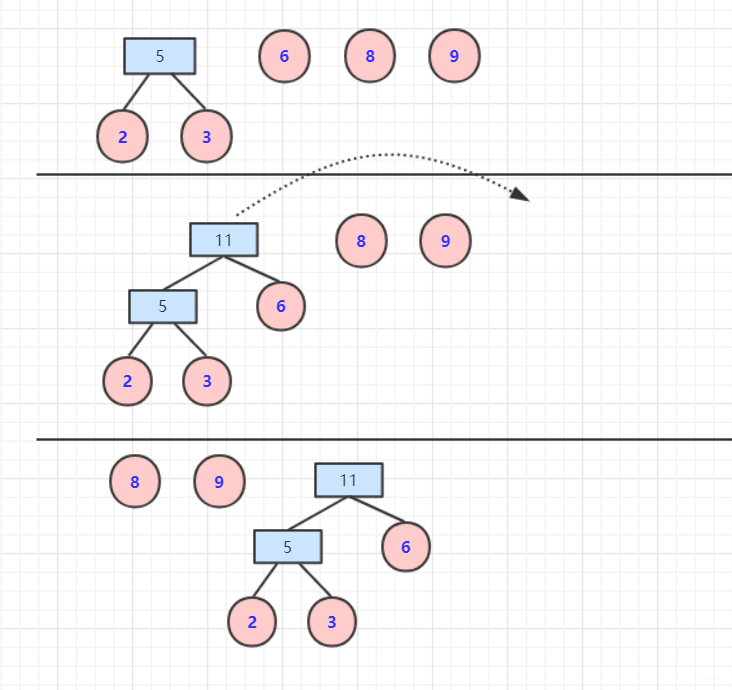
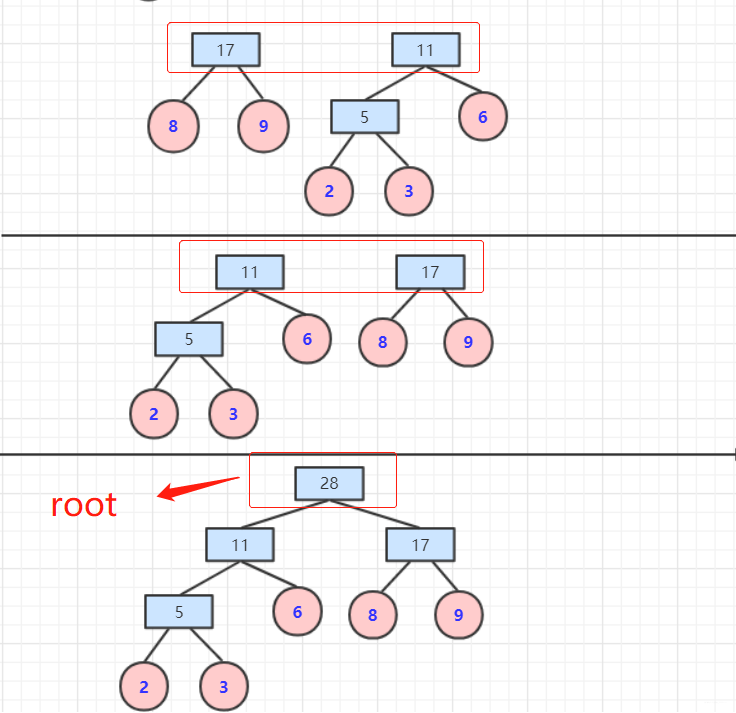
放入优先队列(自己排序也行)每次取两个最小权值顶点,构造父节点(value=left.value+right.value).
- 如果
队列为空,那么返回节点,并且这个节点为根节点root。

- 否则继续加入队列进行排序。重复上述操作,直到队列为空。

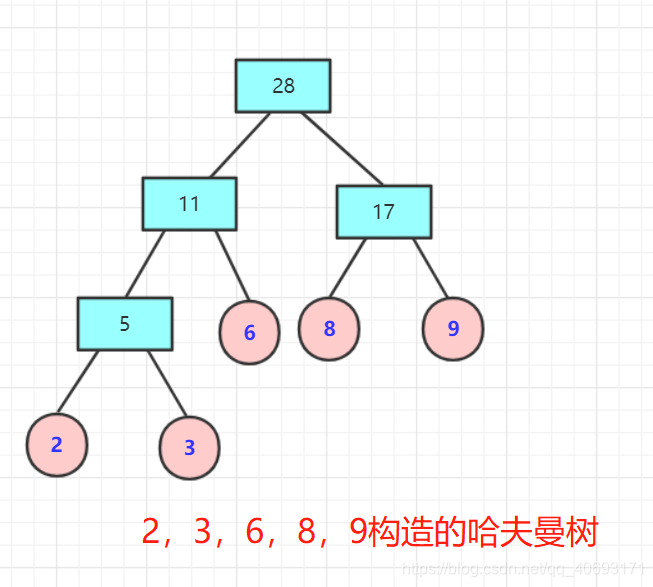
在计算带权路径长度的时候,需要重新计算树的高度(从下往上),因为哈夫曼树是从下往上构造的,所以对于高度不太好维护,可以构造好然后计算高度。
比如上述的WPL为:2*3+3*3+6*2+8*2+9*2=(2+3)*3+(6+8+9)*2=61.
代码实现:
package 二叉树;
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.Comparator;
import java.util.List;
import java.util.PriorityQueue;
import java.util.Queue;
public class HuffmanTree {
public static class node
{
int value;
node left;
node right;
int deep;//记录深度
public node(int value) { this.value=value; this.deep=0;
}
public node(node n1, node n2, int value) { this.left=n1; this.right=n2; this.value=value;
}
}
private node root;//最后生成的根节点
List<node>nodes;
public HuffmanTree() {
this.nodes=null;
}
public HuffmanTree(List<node>nodes)
{
this.nodes=nodes;
}
public void createTree() { Queue<node>q1=new PriorityQueue<node>(new Comparator<node>() {
public int compare(node o1, node o2) { return o1.value-o2.value;
}}); q1.addAll(nodes); while(!q1.isEmpty()) { node n1=q1.poll(); node n2=q1.poll(); node parent=new node(n1,n2,n1.value+n2.value); if(q1.isEmpty()) { root=parent;return; } q1.add(parent); }
}
public int getweight() {
Queue<node>q1=new ArrayDeque<node>();
q1.add(root);
int weight=0;
while (!q1.isEmpty()) { node va=q1.poll(); if(va.left!=null) { va.left.deep=va.deep+1;va.right.deep=va.deep+1; q1.add(va.left);q1.add(va.right); } else { weight+=va.deep*va.value; }
}
return weight;
}
public static void main(String[] args) {
List<node>list=new ArrayList<node>();
list.add(new node(2));
list.add(new node(3));
list.add(new node(6));
list.add(new node(8));list.add(new node(9));
HuffmanTree tree=new HuffmanTree();
tree.nodes=list;
tree.createTree();
System.out.println(tree.getweight());
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83

哈夫曼树还是比较容易理解,主要构造利用贪心算法的思想。代码实现复杂度可能不太高,如果有大佬指正还希望指正!
如果对数据结构,爬虫等感兴趣,还请关注我的公众号:bigsai.一起学习交流!

文章来源: bigsai.blog.csdn.net,作者:Big sai,版权归原作者所有,如需转载,请联系作者。
原文链接:bigsai.blog.csdn.net/article/details/100178860
【版权声明】本文为华为云社区用户转载文章,如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者


评论(0)