矩阵快速幂&求大斐波那契&poj3070（java）

题目链接
核心思想为：

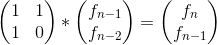
从右往左。可以一直递推，然后到最后一项，然后快速幂求矩阵，矩阵最终的结果就是所求结果。
更新：java的矩阵通用乘法可以表示为，可以将下列代码替换道ac代码中：

import java.util.Scanner;

public class poj3070 { public static void main(String[] args) { // TODO 自动生成的方法存根 Scanner sc=new Scanner(System.in); while(sc.hasNext()) { int n=sc.nextInt(); if(n==-1)break; if(n==0) {System.out.println(0);} else { n-=1;// int a[][]= {{1,1},{1,0}}; int b[][]={{1,0},{0,1}}; int time=0; while(n>0) { if(n%2==1) { b=q(a, b); } a=q(a, a);n/=2; } System.out.println((b[0][0])); } } } static int [][] q(int a[][],int b[][]){// int x=a.length;//a[0].length=b.length 为满足条件 int y=b[0].length;//确定每一排有几个 int c[][]=new int [x][y]; for(int i=0;i<x;i++) for(int j=0;j<y;j++) { //需要确定每一个元素 //c[i][j]; for(int t=0;t<b.length;t++) { c[i][j]+=(a[i][t]%10000)*(b[t][j]%10000); c[i][j]%=10000; } } return c; }
}

  
 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
 

文章来源: bigsai.blog.csdn.net，作者：Big sai，版权归原作者所有，如需转载，请联系作者。

原文链接：bigsai.blog.csdn.net/article/details/84233828