操作系统之进程调度——优先权法和轮转法（附上样例讲解）
操作系统之银行家算法—详解流程及案例数据
操作系统之多线程编程—读者优先/写者优先详解
操作系统之存储管理——FIFO算法和LRU算法
操作系统之磁盘调度——SCAN实例讲解

要求

一、实验目的
多道程序设计中，经常是若干个进程同时处于就绪状态，必须依照某种策略来决定那个进程优先占有处理机。因而引起进程调度。本实验模拟在单处理机情况下的处理机调度问题，加深对进程调度的理解。
二、实验内容
1．优先权法、轮转法
简化假设
1）进程为计算型的（无I/O）
2）进程状态：ready、running、finish
3）进程需要的CPU时间以时间片为单位确定
2．算法描述
1）优先权法——动态优先权
当前运行进程用完时间片后，其优先权减去一个常数。
2）轮转法
三、流程图
优先权：

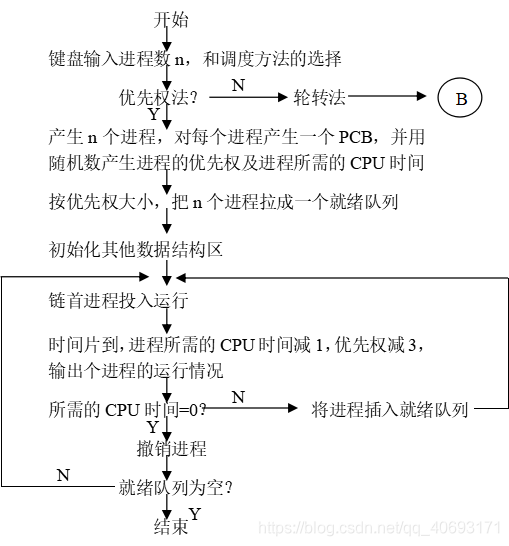
轮转法：

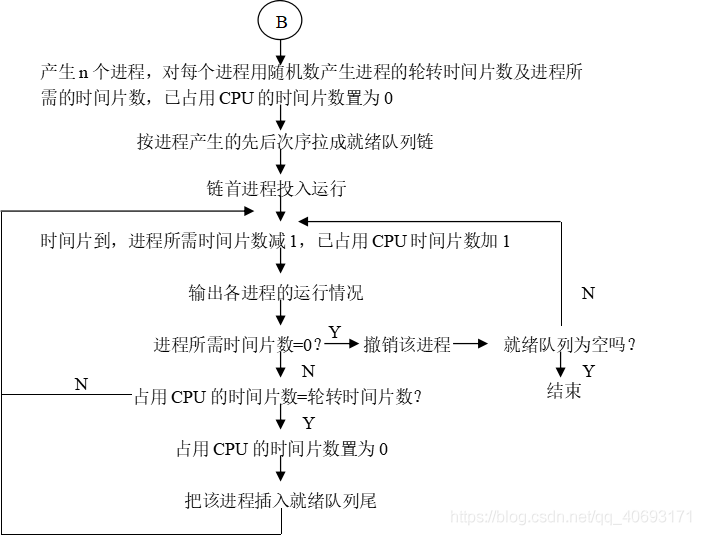
分析

?想要完成操作系统算法第一步要弄清楚操作系统相关的专业术语。弄清各个算法的流程和目的要求。才能模拟出相关算法的过程。下面先附上实验的相关要求?

通过本次实验，深刻的理解了操作系统中线程资源的分配方式和进程的调度方式。操作系统实验重在理解每一个算法的意图和目的，那么就选择适当的数据结构模拟过程就可以完成相关算法了。

优先权算法：

1. 所有线程的序列核心是围绕优先权的权值大小。并且该优先权的大小会动态的变化，那么我们选区以权值为排序准则的优先队列是处理该结构的最好方法。能够有效的节省空间，算法复杂度。
2. 而优先权算法某个线程的结束标识是还需要的时间needtime。所以在随机选区线程的时候和输出状态的时候要判断该线程还需不需要资源。
3. 至于状态还有一点很重要的是要即使转换。当进行下一个操作要即使转换上一个线程的状态和下一个线程的状态防止状态混淆。

轮转法：

• 轮转法强调先进先出的拉链式顺序，而不以其他的权值作为开始/调度的先后顺序，所以普通先进先出的普通队列是解决该算法的最好方法。
• . 轮转法和优先权法不一样的是优先权法每次只进一个线程只执行一次。而轮转法是进一个可以执行最多是该线程可轮转的次数/轮转值（可能在中间就完成线程的释放），所以在写程序的时候每次都要判断是否已经轮转。并且到最后还要判断还是否需要调度。如果需要，再抛入队尾。

代码

实现的代码（java）:

import java.util.ArrayDeque;
import java.util.Comparator;
import java.util.PriorityQueue;
import java.util.Queue;
import java.util.Scanner;

public class priority {

	static pcb pcb[];
	public static void main(String[] args) {
		// TODO 自动生成的方法存根
		System.out.println("创建线程数量：");
		Scanner sc=new Scanner(System.in);
		int n=sc.nextInt();
		pcb=new pcb[n];
		for(int i=0;i<n;i++)
		{ pcb[i]=new pcb(i+1,"ready");
		}
		System.out.println("是否采用优先权？Y/N");
		String s=sc.next();
		if(s.equals("Y"))
		{ priority();
		}
		else
		{ lunzhuan();
		}
		//printstatus();
	}
	private static void lunzhuan() {
		Queue<pcb>q1=new ArrayDeque<>();
		for(int i=0;i<pcb.length;i++)
		{ int lunhzun=(int) (Math.random()*4)+1+(int)(Math.random()*2);//不能为0 int needtime=(int)(Math.random()*8)+1; pcb[i].lunhzuan=lunhzun; pcb[i].needalltime=needtime; q1.add(pcb[i]);
		}
		while(!q1.isEmpty())
		{ pcb team=q1.poll(); int time=0;//占用cpu时间片树 while(time<team.lunhzuan) { if(team.needalltime<=0) {break;} time++; team.needalltime-=1; team.status="running"; printluzhuan(); System.out.println(); } if(team.needalltime<=0) {team.status="finish";} else { team.status="ready"; q1.add(team); }
		}
		printluzhuan();
	}
	private static void printluzhuan() {
		for(int i=0;i<pcb.length;i++)
		{ System.out.println("threadid:"+pcb[i].id+"  "+pcb[i].status+"  needtime:"+pcb[i].needalltime+"  lunzhuan:"+pcb[i].lunhzuan);
		} }
	private static void priority() {//优先权
		Queue<pcb>q1=new PriorityQueue<pcb>(com);
		for(int i=0;i<pcb.length;i++)
		{ int proty=(int) (Math.random()*15); int needtime=(int)(Math.random()*4)+1; pcb[i].proty=proty; pcb[i].needalltime=needtime; q1.add(pcb[i]);
		}	
//		for(int i=0;i<pcb.length;i++)
//		{
//			q1.add(pcb[i]);
//		}
		while(!q1.isEmpty())
		{ pcb team=q1.poll(); team.needalltime-=1; team.proty-=3; team.status="running"; printstatus(); System.out.println(); if(team.needalltime>0) { team.status="ready"; q1.add(team); } else team.status="finish";
		}
		printstatus();
	}
	private static void printstatus() {
		// TODO 自动生成的方法存根
		for(int i=0;i<pcb.length;i++)
		{ System.out.println("threadid:"+pcb[i].id+"  "+pcb[i].status+"  needtime:"+pcb[i].needalltime+"  priority:"+pcb[i].proty);
		} }
	static Comparator<pcb> com=new Comparator<pcb>() {
		@Override
		public int compare(pcb o1, pcb o2) { // TODO 自动生成的方法存根 return o2.proty-o1.proty;
		}
	}; 
	static class pcb
	{ int id;//进程id
		String status;//进程状态
		int proty;
		int needalltime;//需要总时间
		int lunhzuan;//轮转时间树
		public pcb(int id, String status) { // TODO 自动生成的构造函数存根 this.id=id; this.status=status;
		}	
	}
}

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
  
55
  
56
  
57
  
58
  
59
  
60
  
61
  
62
  
63
  
64
  
65
  
66
  
67
  
68
  
69
  
70
  
71
  
72
  
73
  
74
  
75
  
76
  
77
  
78
  
79
  
80
  
81
  
82
  
83
  
84
  
85
  
86
  
87
  
88
  
89
  
90
  
91
  
92
  
93
  
94
  
95
  
96
  
97
  
98
  
99
  
100
  
101
  
102
  
103
  
104
  
105
  
106
  
107
  
108
  
109
  
110
  
111
  
112
  
113
  
114
  
115
  
116
  
117
  
118
  
119
  
120
  
121
  
122
  
123
  
124
  
125
  
126
  
127
  
128
  
129
  
130
  
131
 

数据打印

优先权：

2：轮转法：

声明：这只是本人的个人理解，如果又纰漏，还请大神指出！?

如果对后端、爬虫、数据结构算法等感性趣欢迎关注我的个人公众号交流：bigsai

文章来源: bigsai.blog.csdn.net，作者：Big sai，版权归原作者所有，如需转载，请联系作者。

原文链接：bigsai.blog.csdn.net/article/details/84755887