全排列两种实现方式(java)—poj2718

举报
bigsai 发表于 2021/02/03 01:03:15 2021/02/03
【摘要】 前言 以前遇到的全排列，清一色的dfs回溯，自己知道时间复杂度挺高的，最近遇到poj2718认真总结了下全排列。 全排列：给定几个数，要求找出所有的排列方式。 法一：dfs回溯法： 思路：回溯法的核心思路就是模拟过程，其实它相对简单因为你往往不需要考虑它的下一步是什么，你只需关注如果操作这些数。你往往可能不在意数的规则规律但是也能搞出来。举个例子。有1，2，3...

前言

以前遇到的全排列，清一色的dfs回溯，自己知道时间复杂度挺高的，最近遇到poj2718认真总结了下全排列。
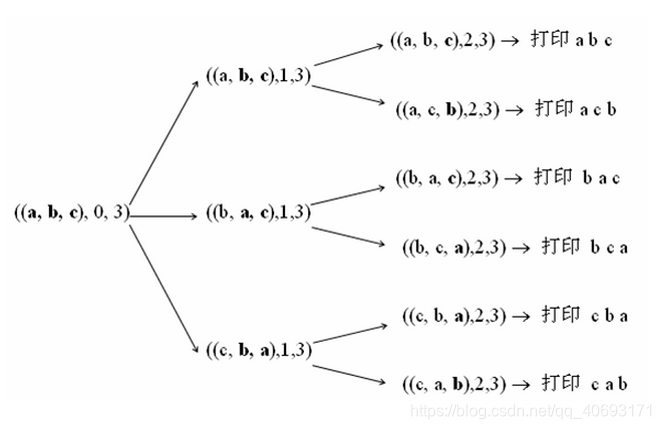
在这里插入图片描述

全排列：给定几个数，要求找出所有的排列方式。

法一：dfs回溯法：

  • 思路：回溯法的核心思路就是模拟过程，其实它相对简单因为你往往不需要考虑它的下一步是什么，你只需关注如果操作这些数。你往往可能不在意数的规则规律但是也能搞出来。
  • 举个例子。有1，2，3，4，5五个数需要全排列。我用回溯法的话我可以用附加的数组，或者list，boolean数组等添加和删除模拟的数据。
  • 比如第一次你可以循环将第一个赋值（1-5）,在赋值每个数的时候标记那些用过，那些还能用的数据，执行dfs一直到底层。然后dfs执行完要将数据复原。比如标记的数据进行取消标记等等。

详细代码为

package 全排列;

import java.util.Scanner;

public class quanpailie1 {
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		String s[] = sc.nextLine().split(" ");
		int a[] = new int[s.length];
		for (int i = 0; i < s.length; i++) { a[i] = Integer.parseInt(s[i]);
		}
		int b[] = new int[a.length];
		boolean b1[] = new boolean[a.length];// 判断是否被用
		long startTime = System.currentTimeMillis();
		dfs(b1, a, b, 0);
		long endTime = System.currentTimeMillis();
		System.out.println("运行时间:" + (endTime - startTime) + "ms");
	}

	private static void dfs(boolean[] b1, int[] a, int b[], int index) {
		// TODO Auto-generated method stub
		int len = a.length;
		if (index == a.length)// 停止
		{ if (b[0] == 0) { } else { for (int j : b) { System.out.print(j + "  "); } System.out.println(); }
		} else for (int i = 0; i < len; i++) { if (!b1[i]) { b[index] = a[i]; b1[i] = true;// 下层不能在用 dfs(b1, a, b, index + 1); b1[i] = false;// 还原 } }

	}
}


  
 
    
  
  • 1
    • 
  
  • 2
    • 
  
  • 3
    • 
  
  • 4
    • 
  
  • 5
    • 
  
  • 6
    • 
  
  • 7
    • 
  
  • 8
    • 
  
  • 9
    • 
  
  • 10
    • 
  
  • 11
    • 
  
  • 12
    • 
  
  • 13
    • 
  
  • 14
    • 
  
  • 15
    • 
  
  • 16
    • 
  
  • 17
    • 
  
  • 18
    • 
  
  • 19
    • 
  
  • 20
    • 
  
  • 21
    • 
  
  • 22
    • 
  
  • 23
    • 
  
  • 24
    • 
  
  • 25
    • 
  
  • 26
    • 
  
  • 27
    • 
  
  • 28
    • 
  
  • 29
    • 
  
  • 30
    • 
  
  • 31
    • 
  
  • 32
    • 
  
  • 33
    • 
  
  • 34
    • 
  
  • 35
    • 
  
  • 36
    • 
  
  • 37
    • 
  
  • 38
    • 
  
  • 39
    • 
  
  • 40
    • 
  
  • 41
    • 
  
  • 42
    • 
  
  • 43
    • 
  
  • 44
    • 
  
  • 45
    • 
  
  • 46
    •

输出打印结果为：

1 2 3 4
1 2 4 3
1 3 2 4
1 3 4 2
1 4 2 3
1 4 3 2
2 1 3 4
2 1 4 3
2 3 1 4
2 3 4 1
2 4 1 3
2 4 3 1
3 1 2 4
3 1 4 2
3 2 1 4
3 2 4 1
3 4 1 2
3 4 2 1
4 1 2 3
4 1 3 2
4 2 1 3
4 2 3 1
4 3 1 2
4 3 2 1
运行时间:2ms

法二：递归法

上述方法虽然能够实现全排列，但是方法的复杂度还是很高。指数级别增长。因为要遍历很多没用的情况。所以当数据较大并不能高速处理。所以换一种思路处理。
设[a,b,c,d]为abcd的全排列
那么，该全排列就是
[1,2,3,4]（四个数的全排列）

  • 1 [2,3,4]（1开头[2,3,4]的全排列）

  • 1 2 [3,4] (1,2开头的[3,4]全排列)

  • 1 2 3 [4] =1 2 3 4(1 2 3 开头的[4]全排列)

  • 1 2 4 [3]=1 2 3 4

  • 1 3 [2,4]

  • 1 3 2 [4]=1 3 2 4

  • 1 3 4 [2]=1 3 4 2

  • 1 4 [3,2]

  • 1 4 3 [2]=1 4 3 2

  • 1 4 2 [3]=1 4 2 3

  • 2 [1,3,4]

  • 2 1 [3,4]

  • 2 1 3 [4]=2 1 3 4

  • 2 1 4 [3]=2 1 4 3

  • 2 3 [1,4]

  • 2 3 1 [4]=2 3 1 4

  • 2 3 4 [1]=2 3 4 1

  • 2 4 [3,1]

  • 2 4 3 [1]=2 4 3 1

  • 2 4 1 [3]=2 4 1 3

  • 3 [2,1,4]=(略)

  • 3 2 [1,4]

  • 3 1 [2,4]

  • 3 4 [3,2]

  • 4 [2,3,1](略)

  • 4 2 [3,1]

  • 4 3 [2,1]

  • 4 1 [3,2]

对于全排列递归的模式为：（和dfs很像）

  • isstop?: 判断递归终止
  • stop
  • do not stop:
  • before recursive()
  • recursive()
  • after recursive()

根据上面的数据找点规律吧：

  1. 上面是递归没毛病。整个全排列就是子排列递归到最后遍历的所有情况
  2. 千万别被用回溯的获得全排列的数据影响。博主之前卡了很久一直想着从回溯到得到的数据中找到递归的关系，结果写着写着就写崩了。
  3. 递归的数据有规律。它只关注位置而不关注数据的大小排列。意思是说你不需要纠结每一种排列的初始态是啥。你只要关注他有那些数就行，举个例子，出台为1 [2,3,4]和1 [4,3,2]的效果一样，你需要关注的是1这个部分。1这个部分处理好递归自然会处理好子节点的关系。
  4. 对于同一层级 比如1[],2[],3[],4[],例如1，2，3，4而言，每一层如下的步骤，可以保证同层数据可靠，并且底层按照如下思路也是正确的。
  • 1,2,3,4—>swap(0,0)—>1 [2 3 4] (子递归不用管)—>swap(0,0)—>1,2,3,4
  • 1,2,3,4—>swap(0,1)—>2 [1 3 4] (子递归不用管)—>swap(0,1)—>1,2,3,4
  • 1,2,3,4—>swap(0,2)—>3 [2 1 4] (子递归不用管)—>swap(0,1)—>1,2,3,4
  • 1,2,3,4—>swap(0,3)—>4 [2 3 1] (子递归不用管)—>swap(0,1)—>1,2,3,4
  1. 所以整个全排列函数大致为：
  • 停止
  • 不停止:
    -for(i from start to end)
  • swap(start,i)//i是从该层后面所有可能的全部要选一次排列到该层
  • recursive(start 1)//该层确定，进入下一层子递归
  • swap(start,i)//因为不能影响同层之间数据，要保证数据都是初始话
    具体代码为：
import java.util.Scanner;

public class quanpailie2 {

	public static void main(String[] args) {
		// TODO Auto-generated method stub Scanner sc = new Scanner(System.in);
		String s[] = sc.nextLine().split(" ");
		int a[] = new int[s.length];
		for (int i = 0; i < s.length; i++) { a[i] = Integer.parseInt(s[i]);
		}
		long startTime = System.currentTimeMillis();
		arrange(a, 0, a.length - 1);
		long endTime = System.currentTimeMillis();
		System.out.println("运行时间:" + (endTime - startTime) + "ms");
	}
	static void arrange(int a[], int start, int end) { if (start == end) { for (int i : a) { System.out.print(i); } System.out.println(); return;
		}
		for (int i = start; i <= end; i++) { swap(a, i, start); arrange(a, start + 1, end); swap(a, i, start);
		}
	}

	static void swap(int arr[], int i, int j) {
		int te = arr[i];
		arr[i] = arr[j];
		arr[j] = te;
	}
}


  
 
    
  
  • 1
    • 
  
  • 2
    • 
  
  • 3
    • 
  
  • 4
    • 
  
  • 5
    • 
  
  • 6
    • 
  
  • 7
    • 
  
  • 8
    • 
  
  • 9
    • 
  
  • 10
    • 
  
  • 11
    • 
  
  • 12
    • 
  
  • 13
    • 
  
  • 14
    • 
  
  • 15
    • 
  
  • 16
    • 
  
  • 17
    • 
  
  • 18
    • 
  
  • 19
    • 
  
  • 20
    • 
  
  • 21
    • 
  
  • 22
    • 
  
  • 23
    • 
  
  • 24
    • 
  
  • 25
    • 
  
  • 26
    • 
  
  • 27
    • 
  
  • 28
    • 
  
  • 29
    • 
  
  • 30
    • 
  
  • 31
    • 
  
  • 32
    • 
  
  • 33
    • 
  
  • 34
    • 
  
  • 35
    • 
  
  • 36
    • 
  
  • 37
    • 
  
  • 38
    • 
  
  • 39
    • 
  
  • 40
    • 
  
  • 41
    •

输入输出结果为：

1 2 3 4
1234
1243
1324
1342
1432
1423
2134
2143
2314
2341
2431
2413
3214
3241
3124
3142
3412
3421
4231
4213
4321
4312
4132
4123
运行时间:1ms

你可以发现两者采用的规则不同，输出的数据到后面是不一样的。但是你可能还没体验到大数据对程序运行的影响。我把输出的结果注释掉。用0 1 2 3 4 5 6 7 8 9进行全排序：
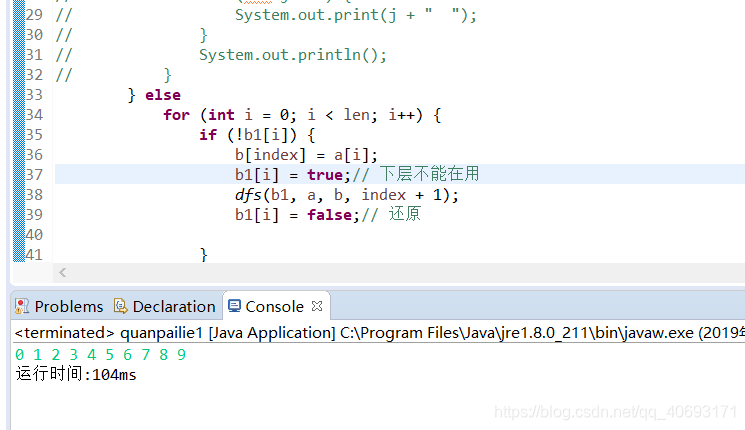
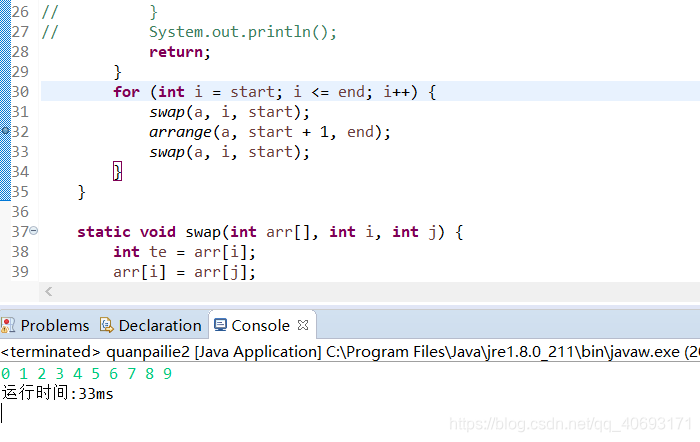
在这里插入图片描述
在这里插入图片描述

对于全排列，建议能采用递归还是递归。因为递归没有额外数组开销。并且计算的每一次都有用。而回溯会有很多无用计算。数只越大越明显。

poj2718

题意就是给几个不重复的数字，让你找出其中所有排列方式中组成的两个数的差值最小。除了大小为0否则0不做开头。

思路：全排列所有情况。最小的一定是该全排列从中间分成2半的数组差。要注意的就是0的处理，不日3个长度的0开头/其他长度的0开头等等。还有的人采用贪心剪枝。个人感觉数据并没有那么有规律贪心不一定好处理，但是你可以适当剪枝减少时间也是可以的。比如根据两个数据的首位 相应剪枝。但这题全排列就可以过。

还有一点就是：数据加减乘除转换，能用int就别用String，string转起来很慢会超时。

附上ac代码，代码可能并不漂亮，前面的介绍也可能有疏漏，还请大佬指出！

package 搜索;

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;

public class poj2718 {

	static int min = Integer.MAX_VALUE;
	static int mid = 0;

	public static void main(String[] args) throws IOException {
		// TODO Auto-generated method stub BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
		PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
		int t = Integer.parseInt(in.readLine());
		for (int q = 0; q < t; q++) { String s[] = in.readLine().split(" "); int a[] = new int[s.length]; for (int i = 0; i < s.length; i++) { a[i] = Integer.parseInt(s[i]); } min = Integer.MAX_VALUE; mid = (a.length) / 2; arrange(a, 0, a.length - 1); out.println(min); out.flush();
		}
	}
	static void arrange(int a[], int start, int end) { if (start == end) {
//			for(int i:a)
//			{
// System.out.print(i);
//			}
//			System.out.println(); if ((a[0] == 0 && mid == 1) || (a[mid] == 0 && a.length - mid == 0) || (a[0] != 0 && a[mid] != 0)) { int va1 = 0; int va2 = 0; for (int i = 0; i < mid; i++) { va1 = va1 * 10 + a[i]; } for (int i = mid; i < a.length; i++) { va2 = va2 * 10 + a[i]; } min = min < Math.abs(va1 - va2) ? min : Math.abs(va1 - va2); } return;
		}
		for (int i = start; i <= end; i++) { swap(a, start, i); arrange(a, start + 1, end); swap(a, start, i);
		}
	}

	static void swap(int arr[], int i, int j) {
		int te = arr[i];
		arr[i] = arr[j];
		arr[j] = te;
	}
}


  
 
    
  
  • 1
    • 
  
  • 2
    • 
  
  • 3
    • 
  
  • 4
    • 
  
  • 5
    • 
  
  • 6
    • 
  
  • 7
    • 
  
  • 8
    • 
  
  • 9
    • 
  
  • 10
    • 
  
  • 11
    • 
  
  • 12
    • 
  
  • 13
    • 
  
  • 14
    • 
  
  • 15
    • 
  
  • 16
    • 
  
  • 17
    • 
  
  • 18
    • 
  
  • 19
    • 
  
  • 20
    • 
  
  • 21
    • 
  
  • 22
    • 
  
  • 23
    • 
  
  • 24
    • 
  
  • 25
    • 
  
  • 26
    • 
  
  • 27
    • 
  
  • 28
    • 
  
  • 29
    • 
  
  • 30
    • 
  
  • 31
    • 
  
  • 32
    • 
  
  • 33
    • 
  
  • 34
    • 
  
  • 35
    • 
  
  • 36
    • 
  
  • 37
    • 
  
  • 38
    • 
  
  • 39
    • 
  
  • 40
    • 
  
  • 41
    • 
  
  • 42
    • 
  
  • 43
    • 
  
  • 44
    • 
  
  • 45
    • 
  
  • 46
    • 
  
  • 47
    • 
  
  • 48
    • 
  
  • 49
    • 
  
  • 50
    • 
  
  • 51
    • 
  
  • 52
    • 
  
  • 53
    • 
  
  • 54
    • 
  
  • 55
    • 
  
  • 56
    • 
  
  • 57
    • 
  
  • 58
    • 
  
  • 59
    • 
  
  • 60
    • 
  
  • 61
    • 
  
  • 62
    • 
  
  • 63
    • 
  
  • 64
    • 
  
  • 65
    • 
  
  • 66
    • 
  
  • 67
    • 
  
  • 68
    •

dfs回溯法github链接
递归法全排列github链接
poj2718代码github链接
如有错误还请大佬指正。

  • 如果对后端、爬虫、数据结构算法等感性趣欢迎关注我的个人公众号交流：bigsai

文章来源: bigsai.blog.csdn.net，作者：Big sai，版权归原作者所有，如需转载，请联系作者。

原文链接：bigsai.blog.csdn.net/article/details/90299747

【版权声明】本文为华为云社区用户转载文章，如果您发现本社区中有涉嫌抄袭的内容，欢迎发送邮件进行举报，并提供相关证据，一经查实，本社区将立刻删除涉嫌侵权内容，举报邮箱： cloudbbs@huaweicloud.com
GitHub Java
  • 点赞
  • 收藏
  • 关注作者

评论（0）

0/1000
抱歉，系统识别当前为高风险访问，暂不支持该操作

全部回复

上滑加载中

设置昵称

在此一键设置昵称，即可参与社区互动！

*长度不超过10个汉字或20个英文字符，设置后3个月内不可修改。

*长度不超过10个汉字或20个英文字符，设置后3个月内不可修改。

确认 取消

加入云驻计划，成为创作者

  • 华为云周边好礼
  • 免费体验产品
  • 特殊身份标识
  • 线下官方门票
  • 内部专家零距离
  • 与10000+优质创作者共同成长
立即加入