数据结构与算法—前导
前言
重要性
- 数据结构与算法是程序员内功体现的重要标准之一,而数据结构的也应用在各个方面,更有
程序=数据结构+算法这个等式存在。各个中间件开发者,架构师。他们都在努力的优化中间件、项目结构以及算法提高运行效率降低内存占用。并且数据结构中也是蕴含模型以及面向对象的思想,掌握数据结构对逻辑思维处理抽象能力有很大提升。。
数据结构
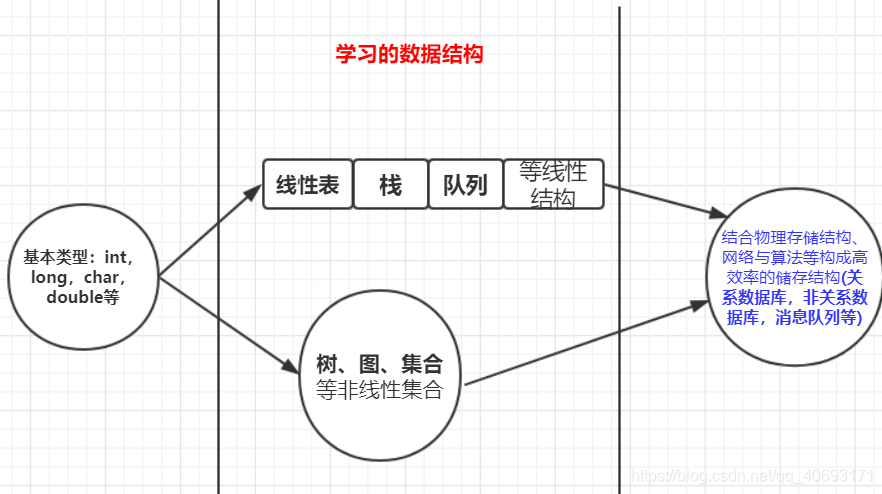
概念
- 数据结构是计算机存储、组织数据的方式。数据结构是指相互之间存在一种或多种特定关系的数据元素的集合。通常情况下,精心选择的数据结构可以带来更高的运行或者存储效率。
个人理解
- 简言之,数据结构是一系列的存储结构按照一定
执行规则、配合一定执行算法所形成的高效的存储结构。在我们所熟知的关系数据库、非关系数据库、搜索引擎存储、消息队列等都是比较牛的大型数据结构良好的运用。这些数据结构应用不仅仅考虑到内存范围结构设计。还考虑实际os、网络等其他因素。 - 而对于数据结构与算法这个专栏。我们程序员更改掌握的首先是在
内存中运行的抽象的数据结构。是一个相对比较单一的数据结构类型,比如线性结构、树、图等等.
相关术语
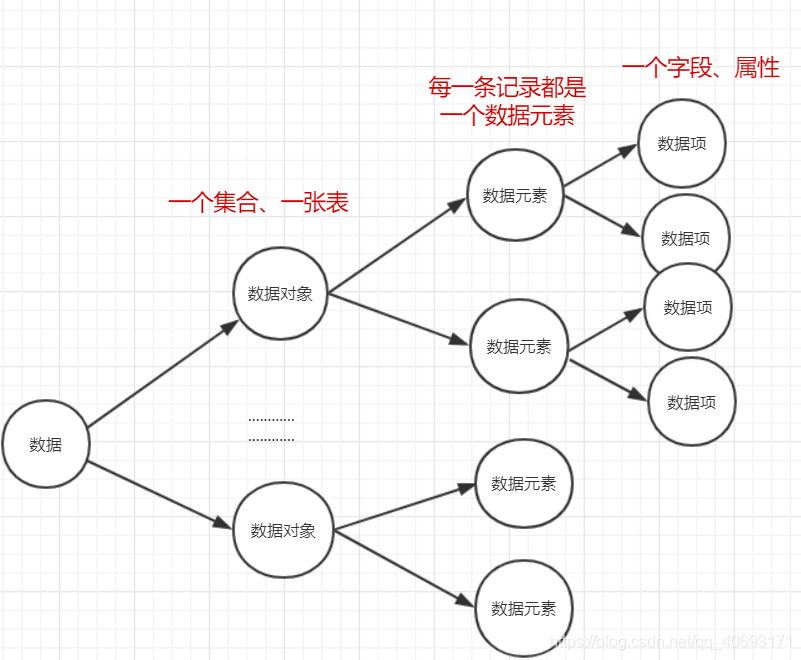
用户信息表users
| id | name | sex |
|---|---|---|
| 001 | bigsai | man |
| 002 | smallsai | man |
| 003 | 菜虚鲲 | woman |
users的pojo对象
class users
{ //略 int id; String name; String sex;
}
//list和woman是数据
List<users>list;//数据对象list
List<users>woman;//数据对象woman
list.add(new users(001,"bigsai","man"));//添加数据元素 一个users由(001,bigsai,man)三个数据项组成
list.add(new users(002,"smallsai","man"));//数据元素
list.add(new users(003,"菜虚鲲","woman"));//数据元素
woman.add(list.get(2));//003,"菜虚鲲","woman"三个数据项构成的一个数据元素
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 数据:对客观事物的符号表示,指所有能输入到计算机中并被计算机程序处理的符号的集合总称。
上述表中的三条用户信息的记录就是数据(也可能多表多集合)。这些数据一般都是用户输入或者是自定义构造完成。当然,还有一些图像、声音也是数据。 - 数据元素:数据元素是数据的
基本单位。一个数据元素由若干数据项构成!可认为是一个pojo对象、或者是数据库的一条记录。比如菜虚鲲那条记录就是一个数据元素。 - 数据项: 而构成用户字段/属性的有
id、name、sex等,这些就是数据项.数据项是构成数据元素的最小不可分割字段。可以看作一个pojo对象或者一张表(people)的一个属性/字段的值。 - 数据对象:是相同性质数据元素的集合。是数据的一个子集。比如上面的
users表、list集合、woman集合都是数据对象。单独一张表,一个集合都可以是一个数据对象。 - 数据类型
原子类型:其值不可再分的类型。比如int,char,double,float等。结构类型:其值可以再分为若干成分的数据类型。比如结构体构造的各种结构等。
- 抽象数据类型(ADT):抽象数据类型(ADT)是一个实现包括储存数据元素的存储结构以及实现基本操作的算法。使得只研究和
使用它的结构而不用考虑它的实现细节成为可能。比如我们使用Arraylist。二叉树等等只需要new 一个而不需要去具体考虑他的内部实现方式。只需要了解他的api和性质即可。其实各个框架的思想也是这样,对数据、接口进行封装、继承使得我们只需要会用而不需要弄清楚它的具体实现细节。
三要素
- 逻辑结构:数据元素之间的
逻辑关系。逻辑结构分为线性结构和非线性结构。线性结构就是顺序表、链表之类。而非线性就是集合、树、图这些结构。 - 存储结构:数据结构在计算机中的表示(又称映像,也称物理结构),存储结构主要分为
顺序存储、链式存储、索引存储和散列(哈希)存储。 - 数据的运算:施加在数据上的运算包括运算的
定义和实现,运算的定义基于逻辑结构,运算的实现基于存储结构。
- 在这里
容易混淆的是逻辑结构与存储结构的概念。对于逻辑结构,不难看得出逻辑二字。逻辑关系也就是两者存在数据上的关系而不考虑物理地址的关系。比如线性结构和非线性结构,它描述的是一组数据中的联系方式和形式,他针对的是数据。而存储结构就是跟物理地址挂钩的。比如同样是线性表,可能有多种存储结构的实现方式。比如顺序表和链表(Arraylist,Linkedlist)它们的存储结构就不同并且采用不同存储结构在不同场景计算机运算次数和效率不同。它关注的是计算机物理地址与运行具体实现方式。
算法分析

五个重要特性
- 至于算法的概念,传统的数据结构介绍都会有:
有穷性、确定性、可行性、输入、输出。这些从字面意思即可理解。 - 而一个好的算法,通常更要着重考虑的是
效率和空间资源占用。
算法效率的度量
通常复杂度更多描述的是一个量级程度而很少用具体数字描述。
空间复杂度
概念:是对一个算法在运行过程中临时占用存储空间大小的量度,记做S(n)=O(f(n))
-
空间复杂度其实在算法的衡量占比是
比较低的,但是不能忽视空间复杂度中重要性。无论在刷题还是实际项目生产内存都是一个极大额指标。对于java而言更是如此。本身内存就大,如果采用的存储逻辑不太好会占用更多的系统资源,对服务造成压力。 -
而算法很多情况都是牺牲空间换取时间(效率)。就比如我们熟知的字符串匹配
String.contains()方法,我们都知道他是暴力破解,时间复杂度为O(n2),不需要借助额外内存。而KMP算法在效率和速度上都原生暴力方法,但是KMP要借助其他数组(next[])进行标记储存运算。就用到了空间开销。再比如归并排序也会借助新数组在递归分冶的适合进行逐级计算。提高效率,而增加内存开销。 -
当然,你的时间算法的空间花销最大不能超过jvm设置的最大值,一般为2G.(2147483645)如果开二维数组多种多维数据不要开的太大,可能会导致
heap OutOfMemoryError。
时间复杂度*
概念:计算机科学中,算法的时间复杂度是一个函数,它定性描述了该算法的运行时间。这是一个关于代表算法输入值的字符串的长度的函数。时间复杂度常用大O符号表述,不包括这个函数的低阶项和首项系数。使用这种方式时,时间复杂度可被称为是渐近的,它考察当输入值大小趋近无穷时的情况。
时间复杂度的排序:O(1) < O(logn) < O(n) < O(nlogn) < O(n2) < O(n3) < O(2n) <O(n!) < O(nn)
常见时间复杂度:对于时间复杂度,很多人的概念是比较模糊的。下面举例子说明一些时间复杂度。
O(1): 常数函数
a=15
O(logn): 对数函数
for(int i=1;i<n;i*=2)
分析:假设执行t次使得i=n;有2t=n; t=log2n,为log级别时间复杂度为O(logn)。- 还有二分查找,拓展欧几里得,快速幂等算法均为O(logn)(曾记录过)。属于高效率算法。
O(n): 线性函数
for (int i=0;i<n;i++)- 比较常见,能够良好解决大部分问题。
O(nlogn):
for (int i=1;i<n;i++)
for (int j=1;j<i;j*=2)- 常见的排序算法很多正常情况都是nlogn。
O(n2)
for(int i=0;i<n;i++)
for(int j=0;j<i;j++)- 其实O(n2)的效率就不敢恭维了。对于大的数据O(n2)甚至更高次方的执行效果会很差。
当然如果同样是n=10000.那么不同时间复杂度额算法执行次数、时间也不同。
| 具体 | n | 执行次数 |
|---|---|---|
| O(1) | 10000 | 1 |
| O(log2n) | 10000 | 14 |
| O( n1/2) | 10000 | 100 |
| O(n) | 10000 | 10000 |
| O(nlog2n) | 10000 | 140000 |
| O(n2) | 10000 | 100000000 |
| O(n3) | 10000 | 1000000000000 |
- 当然有些复杂度靠先天
结构优势,比如树的查找,线段树的动态排序等等。还有的是靠算法策略解决,比如同样是排序,冒泡排序的地位就略低,还有dp算法用动态发现规律解决问题。要想变得更快,那就得掌握更高级的数据结构和更精巧的算法。
时间复杂度计算
时间复杂度计算一般步骤:
- 1、找到执行次数最多的语句
2、计算语句执行的数量级
3、用O表示结果
两个规则:
- 加法规则: 同一程序下如果多个
并列关系的执行语句那么取最大的那个。
eg:T(n)=O(m)+O(n)=max(O(m),O(n));
T(n)=O(n)+O(nlogn)=max(O(n),O(nlogn))=O(nlogn); - 乘法规则:循环结构,时间复杂度按乘法进行计算
eg:T(n)=O(m)*O(n)=O(mn)
·T(n)=O(m)*O(m)=O(m^2)(两层for循环)
其他:
- 当然有些算法的时间复杂度还跟输入的数据有关,分为还会有
最优时间复杂度(可能执行次数最少时),最坏时间复杂度(执行次数最少时),平均时间复杂度.这在后面的排序算法会具体分析。
当然,后面会一起学习一些常见的数据结构和常见的算法,进行复杂度剖析。至于绪论,就先介绍这些,下面会先介绍线性表和递归算法。
- 欢迎关注我的个人公众号:
bigsai

.
文章来源: bigsai.blog.csdn.net,作者:Big sai,版权归原作者所有,如需转载,请联系作者。
原文链接:bigsai.blog.csdn.net/article/details/96913019
- 点赞
- 收藏
- 关注作者



评论(0)