数据结构与算法—队列详解
【摘要】
目录
前言 队列介绍基本属性 普通队列循环队列链式实现
具体实现数组实现链式实现測試
总结
前言
栈和队列是一对好兄弟，前面我们介绍过数据结构与算法—栈详解，那么栈的机制相对简单，后入先出，就像进入一个狭小的山洞，山洞只有一个出口，只能后进先出(在外面的先出去)。而队列就好比是一个隧道，后面的人跟着前面走，前面人先出去(先入先出)。日常的排队就...
前言
栈和队列是一对好兄弟，前面我们介绍过数据结构与算法—栈详解，那么栈的机制相对简单，后入先出，就像进入一个狭小的山洞，山洞只有一个出口，只能后进先出(在外面的先出去)。而队列就好比是一个隧道，后面的人跟着前面走，前面人先出去(先入先出)。日常的排队就是队列运转形式的一个描述！- 所以队列的
核心理念就是：先进先出！ - 队列的概念：队列是一种特殊的
线性表，特殊之处在于它只允许在表的前端（front）进行删除操作，而在表的后端（rear）进行插入操作，和栈一样，队列是一种操作受限制的线性表。进行插入操作的端称为队尾，进行删除操作的端称为队头。 - 同时，阅读本偏文章最好先弄懂顺序表的基本操作和栈的数据结构！学习效果更佳！
队列介绍
基本属性
队头front：
- 删除数据的一端。对于数组，
从后面插入更容易，前面插入较困难，所以一般用数组实现的队列队头在前面。(删除直接index游标前进，不超过队尾即可)。而对于链表。插入删除在两头分别进行那么头部(前面)删除尾部插入是最方便的选择。
队尾rear：
- 插入数据的一端，同上，在数组和链表中
通常均在尾部位置。当然，其实数组和链表的front和rear还有点小区别，后面会具体介绍。
enQueue(入队)：
- 在
队尾rear插入元素
deQueue(出队)：
- 在
对头front删除元素
普通队列
按照上述的介绍，我们很容易知道数组实现的方式。用数组模拟表示队列。要考虑初始化，插入，问题。
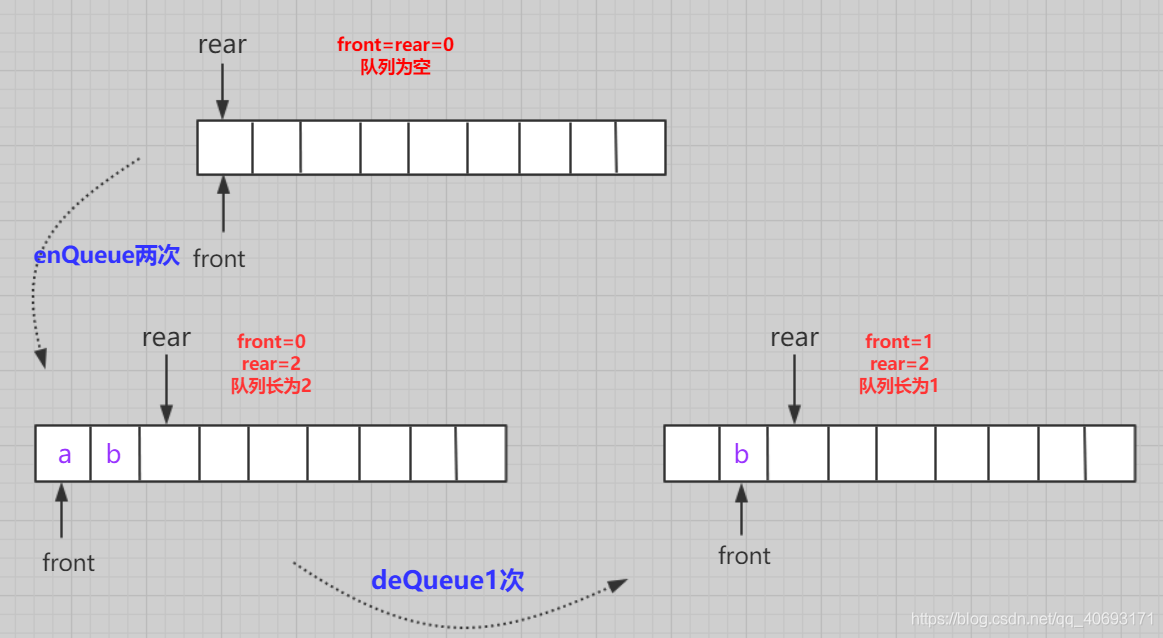
- 初始化：数组的front和rear都指向0.
- 入队：
队不满，数组不越界，先队尾位置传值，再队尾下标+1 - 出队：队不空，先取队头位置元素，在队头+1，
但是很容易发现问题，每个空间域只能利用一次。造成空间极度浪费。并且非常容易越界！
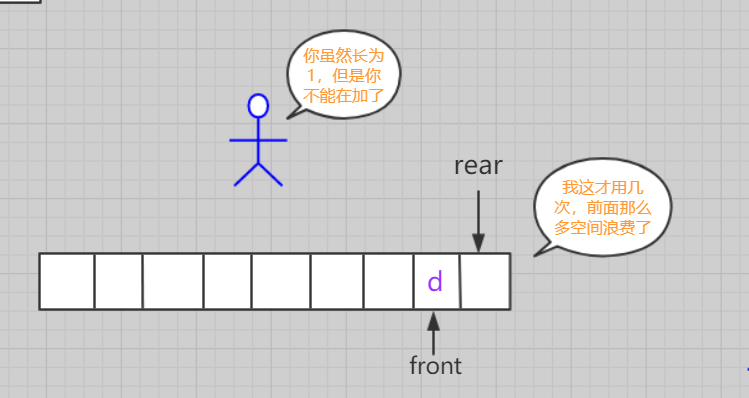
循环队列
针对上述的问题。有个较好的解决方法！就是对已经申请的(数组)内存
重复利用。这就是我们所说的循环队列。
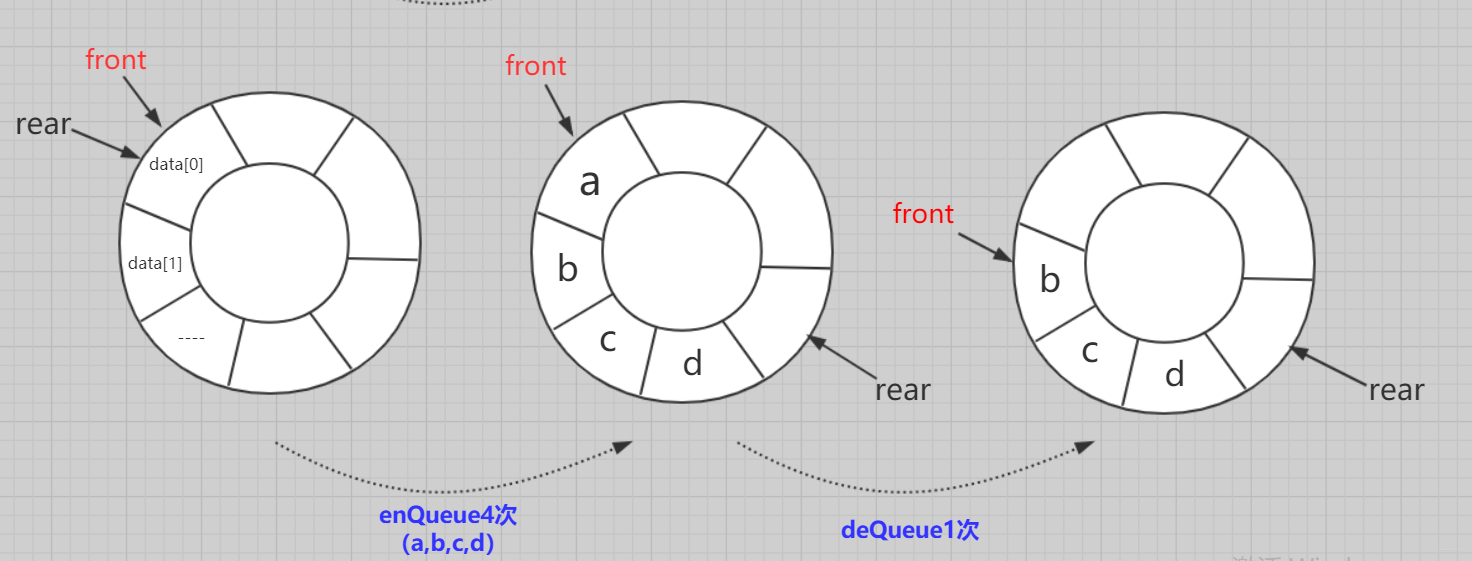
而数组实现的循环队列就是在逻辑上稍作修改。我们假设(约定)数组的最后一位的下一个index是首位。因为我们队列中只需要front和tail两个指标。不需要数组的实际地址位置相关数据。和它无关。所以我们就只需要考虑尾部的特殊操作即可。
- 初始化：数组的front和rear都指向0.
- 入队：
队不满，先队尾位置传值，再rear=(rear + 1) % maxsize; - 出队：队不空，先取队头位置元素，
front=(front + 1)%maxsize; - 是否为空：
return rear == front; - 大小：
return (rear+maxsize-front)%maxsize;
这里面有几个大家需要注意的，就是指标相加如果遇到最后需要转到头的话。可以判断是否到数组末尾位置。也可以直接+1求余。其中maxsize是数组实际大小。
链式实现
对于链表实现的队列，要根据
先进先出的规则考虑头和尾的位置
我们知道队列是先进先出的，对于链表，我们能采用单链表尽量采用单链表，能方便尽量方便，同时还要兼顾效率。
-
方案一 如果队头设在
链表尾，队尾设在链表头。那么队尾进队插入在链表头部插入没问题。容易实现，但是如果队头删除在尾部进行，如果不设置尾指针要遍历到队尾，但是设置尾指针删除需要将它指向前驱节点那么就需要双向链表。都挺麻烦的。 -
方案二但是如果队头设在
链表头，队尾设在链表尾部，那么队尾进队插入在链表尾部插入没问题(用尾指针可以直接指向next)。容易实现，如果队头删除在头部进行也很容易，就是我们前面常说的头节点删除节点。 -
所以我们
最终采取的是方案2的带头节点，带尾指针的单链表!
主要操作为：
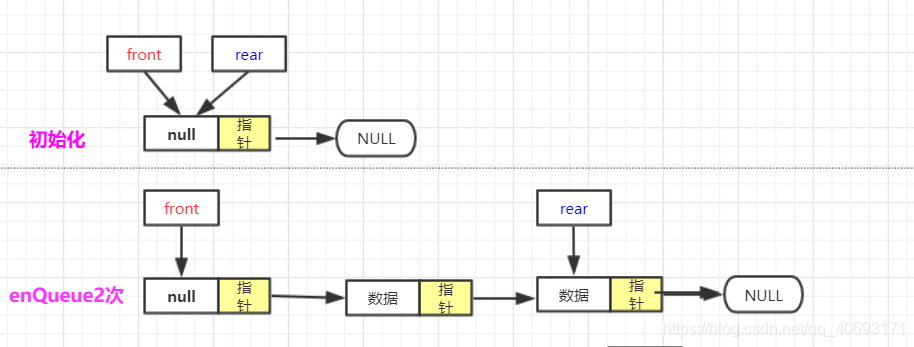
- 初始化：
public class listQueue<T> {
static class node<T> {
T data;// 节点的结果
node next;// 下一个连接的节点
public node() {}
public node(T data) { this.data = data;
}
}
node front;//相当于head 带头节点的
node rear;//相当于tail/end
public listQueue() {
front=new node<T>();
rear=front;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 入队：
rear.next=va;rear=va;（va为被插入节点）
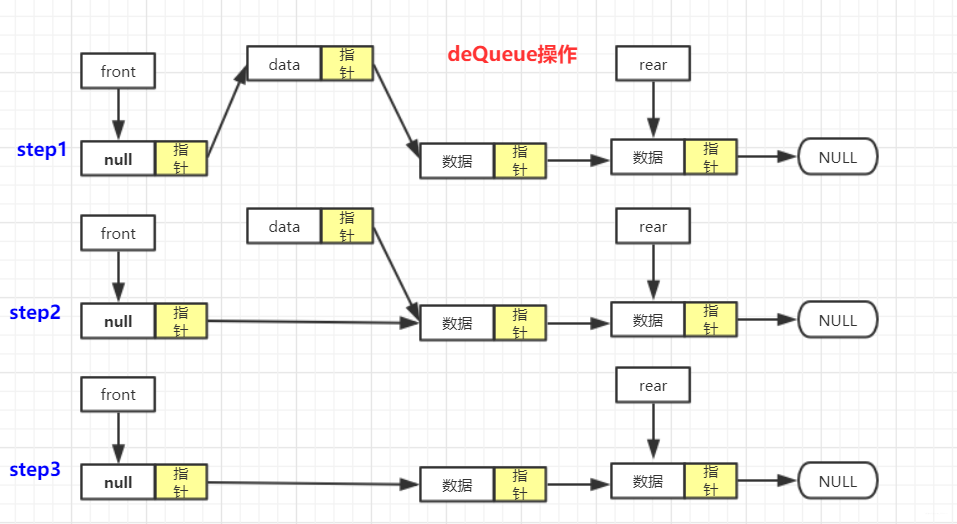
- 出队：队不空，
front.next=front.next.next;经典带头节点删除
- 是否为空：
return rear == front; - 大小：节点front遍历到rear的个数。
具体实现
数组实现
package 队栈;
public class seqQueue<T> {
private T data[];// 数组容器
private int front;// 头
private int rear;// 尾
private int maxsize;// 最大长度
public seqQueue(int i)// 设置长为i的int 型队列
{
data = (T[]) new Object[i+1];
front = 0;
rear = 0;
maxsize = i+1;
}
public int lenth() {
return (rear+maxsize-front)%maxsize;
}
public boolean isempty() {
return rear == front;
}
public boolean isfull() {
return (rear + 1) % maxsize == front;
}
public void enQueue(T i) throws Exception// 入队
{
if (isfull()) throw new Exception("已满");
else { data[rear] = i; rear=(rear + 1) % maxsize;
}
}
public T deQueue() throws Exception// 出队
{
if (isempty()) throw new Exception("已空");
else { T va=data[front]; front=(front+1)%maxsize; return va;
}
}
public String toString()// 输出队
{
String va="队头: ";
int lenth=lenth();
for(int i=0;i<lenth;i++)
{ va+=data[(front+i)%maxsize]+" ";
}
return va;
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
链式实现
package 队栈;
public class listQueue<T> {
static class node<T> {
T data;// 节点的结果
node next;// 下一个连接的节点
public node() {}
public node(T data) { this.data = data;
}
}
node front;//相当于head 带头节点的
node rear;//相当于tail/end
public listQueue() {
front=new node<T>();
rear=front;
}
public int lenth() {
int len=0;
node team=front;
while(team!=rear)
{ len++;team=team.next;
}
return len;
}
public boolean isempty() {
return rear == front;
}
public void enQueue(T value) // 入队.尾部插入
{
node va=new node<T>(value);
rear.next=va;
rear=va;
}
public T deQueue() throws Exception// 出队
{
if (isempty()) throw new Exception("已空");
else { T va=(T) front.next.data; front.next=front.next.next; return va;
}
}
public String toString()
{
node team=front.next;
String va="队头： ";
while(team!=null)
{ va+=team.data+" "; team=team.next;
}
return va;
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
測試
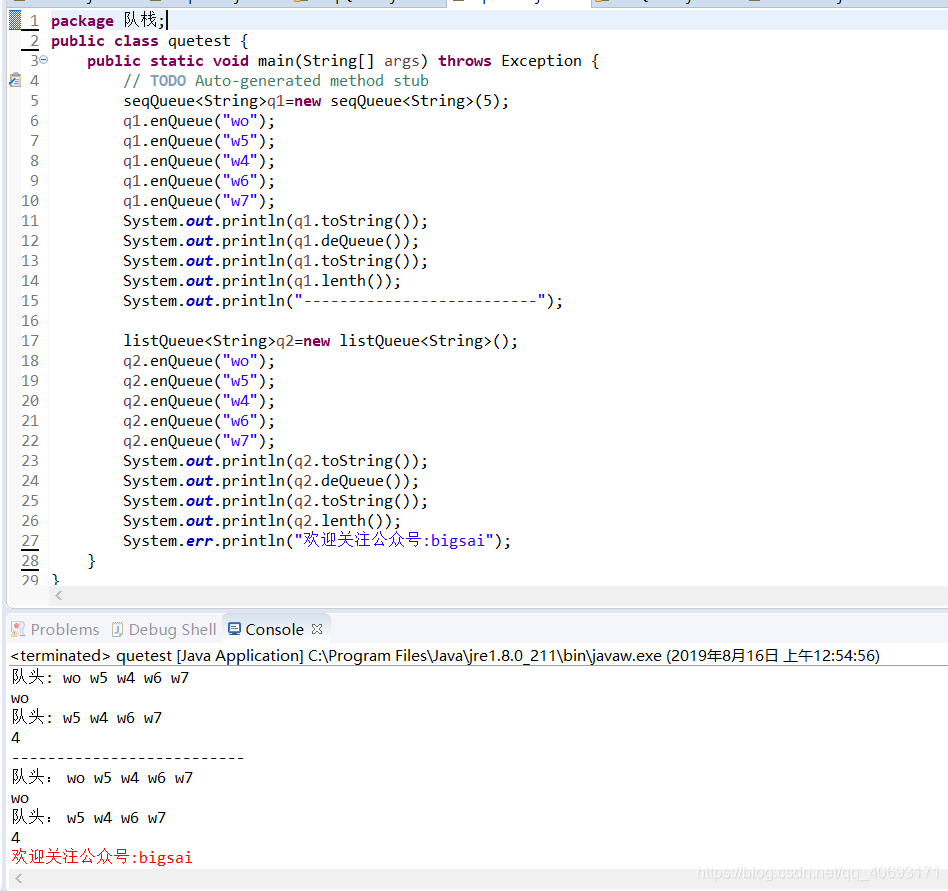
总结
- 对于队列来说数据结构
相比栈复杂一些，但是也不是很难，搞懂先进先出然后就用数组或者链表实现即可。 - 对于数组，队尾
tail指向的位置是空的，而链表的front（head一样）为头指针为空的，所以在不同结构实现相同效果的方法需要注意一下。 - 对于双向队列，大家可以自行了解，双向队列两边均可插入删除，能够实现
堆栈公用等更加灵活调用的结果。(参考java的ArrayDeque).并且现在的消息队列等很多中间件都是基于队列模型延申。所以学会队列很重要！ - 最后，笔者水平有限，如果有
纰漏和不足之处还请指出。另外，如果感觉不错可以点个赞，关注个人公众号：bigsai更多经常与你分享，关注回复数据结构获取精心准备的数据结构和算法资料多份！
文章来源: bigsai.blog.csdn.net，作者：Big sai，版权归原作者所有，如需转载，请联系作者。
原文链接：bigsai.blog.csdn.net/article/details/99617776
【版权声明】本文为华为云社区用户转载文章，如果您发现本社区中有涉嫌抄袭的内容，欢迎发送邮件进行举报，并提供相关证据，一经查实，本社区将立刻删除涉嫌侵权内容，举报邮箱：
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者
评论（0）