目录

一、题目内容

二、解题思路

三、代码

一、题目内容

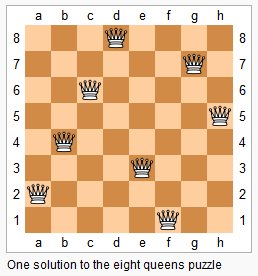
n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

上图为 8 皇后问题的一种解法。

给定一个整数 n，返回所有不同的 n 皇后问题的解决方案。

每一种解法包含一个明确的 n 皇后问题的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

示例：

输入：4
输出：[
 [".Q..",  // 解法 1
  "...Q",
  "Q...",
  "..Q."],

 ["..Q.",  // 解法 2
  "Q...",
  "...Q",
  ".Q.."]
]
解释: 4 皇后问题存在两个不同的解法。

提示：

皇后彼此不能相互攻击，也就是说：任何两个皇后都不能处于同一条横行、纵行或斜线上。

二、解题思路

DFS+回溯，逐行检查皇后位置（横行、纵行或斜线）

三、代码

  

   

    

     

    
    

     

      class Solution:
     
    
   

    

     

    
    

     
 def solveNQueens(self, n: int):
     
    
   

    

     

    
    

     

       res = []
     
    
   

    

     

    
    

     

       path = [['.' for _ in range(n)] for _ in range(n)]
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 def print_path():
     
    
   

    

     

    
    

     
 for i in range(n):
     
    
   

    

     

    
    

     

       print(path[i])
     
    
   

    

     

    
    

     

       print('\n')
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 def change_style(path):
     
    
   

    

     

    
    

     

       new_path = []
     
    
   

    

     

    
    

     
 for i in range(n):
     
    
   

    

     

    
    

     

       cow_path = ''
     
    
   

    

     

    
    

     
 for j in range(n):
     
    
   

    

     

    
    

     

       cow_path += path[i][j]
     
    
   

    

     

    
    

     

       new_path.append(cow_path)
     
    
   

    

     

    
    

     
 return new_path
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 def isValid(r, c):
     
    
   

    

     

    
    

     
 for i in range(1, r + 1):
     
    
   

    

     

    
    

     
 if path[r - i][c] == 'Q':
     
    
   

    

     

    
    

     
 return False
     
    
   

    

     

    
    

     
 if c - i >= 0 and path[r - i][c - i] == 'Q':
     
    
   

    

     

    
    

     
 return False
     
    
   

    

     

    
    

     
 if c + i < n and path[r - i][c + i] == 'Q':
     
    
   

    

     

    
    

     
 return False
     
    
   

    

     

    
    

     
 return True
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 def dfs(pos: int):
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 if pos == n:
     
    
   

    

     

    
    

     

       change_style_path = change_style(path)
     
    
   

    

     

    
    

     

       res.append(change_style_path)
     
    
   

    

     

    
    

     
 return
     
    
   

    

     

    
    

     
 for i in range(n):
     
    
   

    

     

    
    

     
 if isValid(pos, i):
     
    
   

    

     

    
    

     

       path[pos][i] = 'Q'
     
    
   

    

     

    
    

     
 # print_path()
     
    
   

    

     

    
    

     

       dfs(pos + 1)
     
    
   

    

     

    
    

     

       path[pos][i] = '.'
     
    
   

    

     

    
    

     
 # print_path()
     
    
   

    

     

    
    

     

       dfs(0)
     
    
   

    

     

    
    

     
 return res
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      if __name__ == '__main__':
     
    
   

    

     

    
    

     

       n = 4
     
    
   

    

     

    
    

     

       ans_org = [['.', 'Q', '.', '.'],
     
    
   

    

     

    
    

     

       ['.', '.', '.', 'Q'],
     
    
   

    

     

    
    

     

       ['Q', '.', '.', '.'],
     
    
   

    

     

    
    

     

       ['.', '.', 'Q', '.']]
     
    
   

    

     

    
    

     

       s = Solution()
     
    
   

    

     

    
    

     

       ans = s.solveNQueens(n)
     
    
   

    

     

    
    

     

       print(ans)
     
    
  
 

文章来源: nickhuang1996.blog.csdn.net，作者：悲恋花丶无心之人，版权归原作者所有，如需转载，请联系作者。

原文链接：nickhuang1996.blog.csdn.net/article/details/108377958