硬核！手写一个优先队列

文章收录在首发公众号：bigsai 期待你的到访！

前言

事情还要从一个故事讲起：

对于上面那只可爱的小狗狗不会，本篇即为该教程，首先，我要告诉这只可爱的小狗狗，这种问题你要使用的数据结构为优先队列，每次操作的时间复杂度为O(logn),而整个过程的时间复杂度为O(nlogn).

对于本片的设计与实现和堆排序可能有些相似，因为他们都借助堆来实现算法和数据结构，下面详细介绍优先队列的设计与实现。

堆

而堆就是一类特殊的数据结构的统称。堆通常是一个可以被看做一棵树(完全)的数组对象。且总是满足以下规则：

• 堆总是一棵完全二叉树
• 每个节点总是大于(或小于)它的孩子节点。

对于完全二叉树，我想大家都能明白，就是最底层叶子节点要严格按照从左向右来。

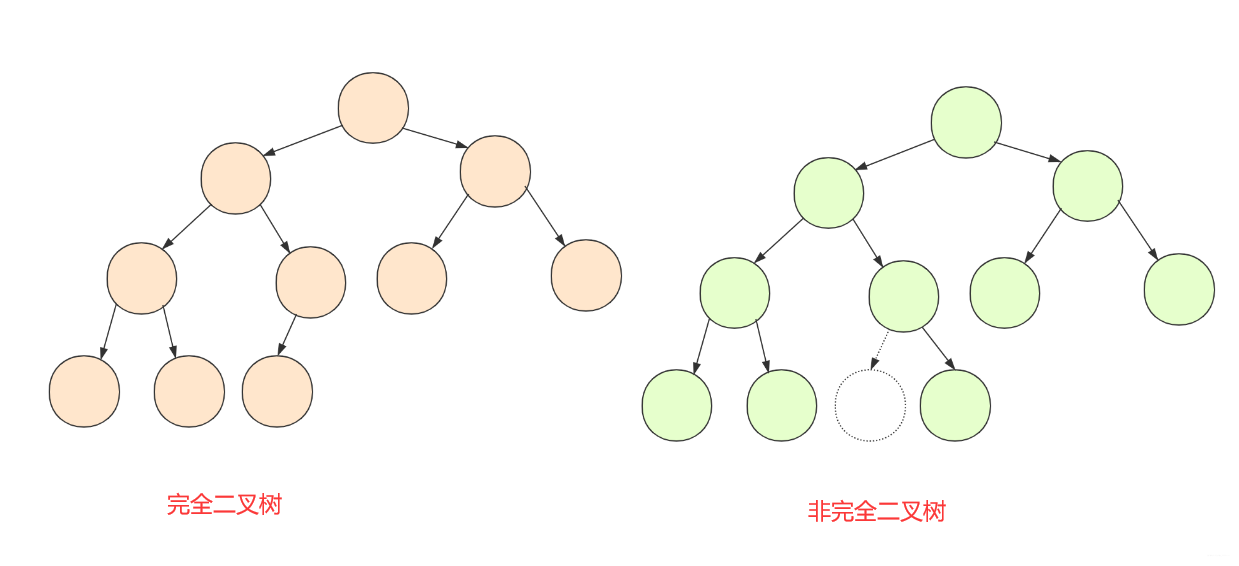
堆有大根堆和小根堆，如果是所有父节点都大于子节点的时候，那么这就是个大根堆，反之则为小根堆，以下就是一个大根堆：

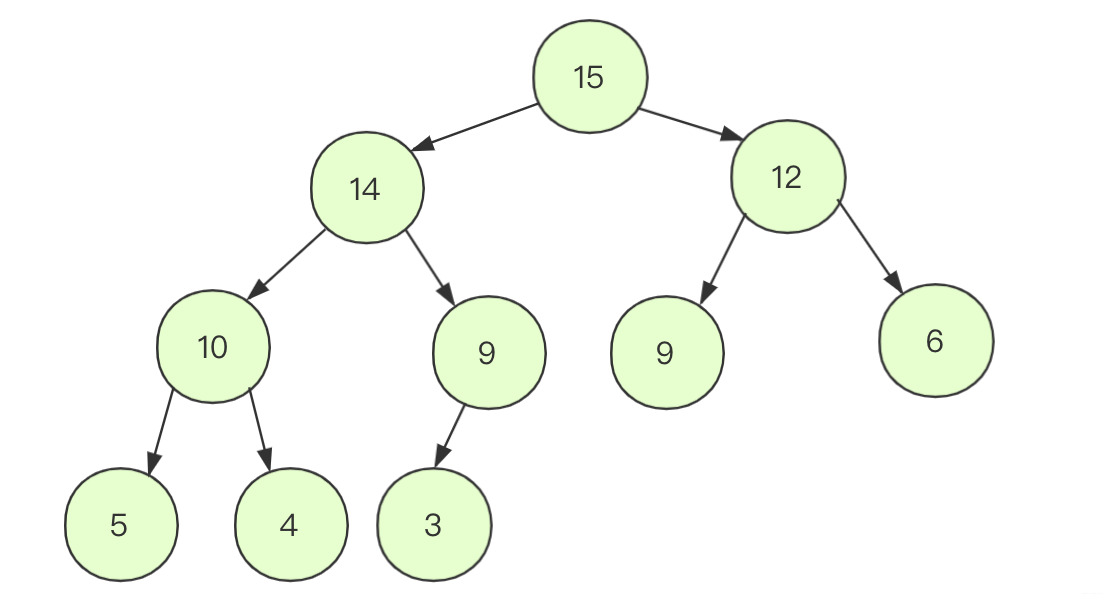
最后需要注意的是我们并不是用链式去储存这个二叉树而是用数组去存储这个树，虽然链式的使用场景可能更多一些，但是在完全二叉树的情况下空间使用率较好没有斜树的出现。并且在操作的时候可以直接通过编号找到位置进行交换。

优先队列

如何理解优先队列，我们先从一段对话说起：

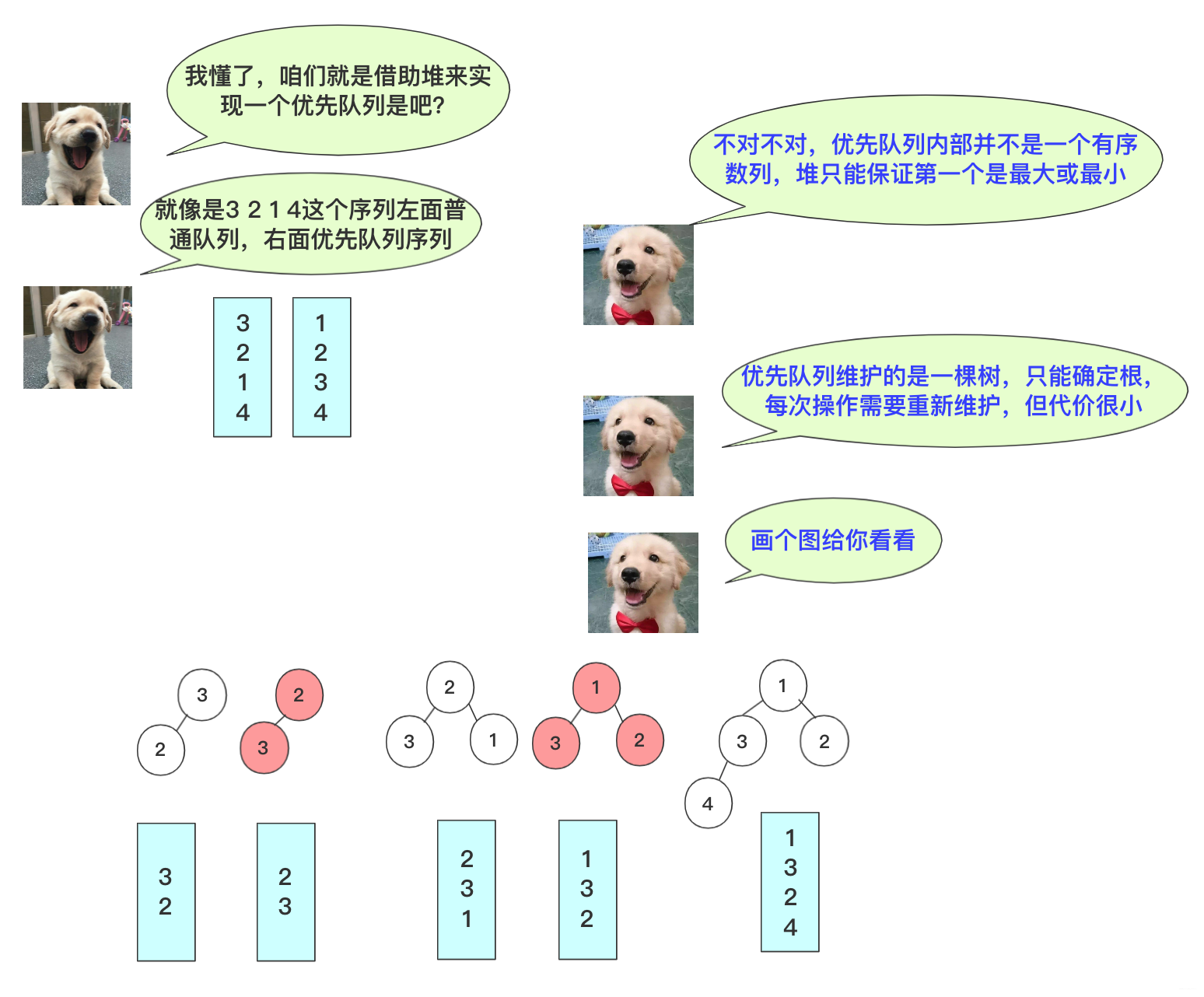
优先队列，它是一个队列。而普通的队列遵从先进先出的规则。而优先队列遵循一个排序的规则：每次抛出自定义排序最大(小)的，默认的情况是抛出最小的，本篇也就从最基本的原理进行分析。

并且它的用法队列还是一样的，，所以我们在设计这个类的时候api方面要与队列的api一致。

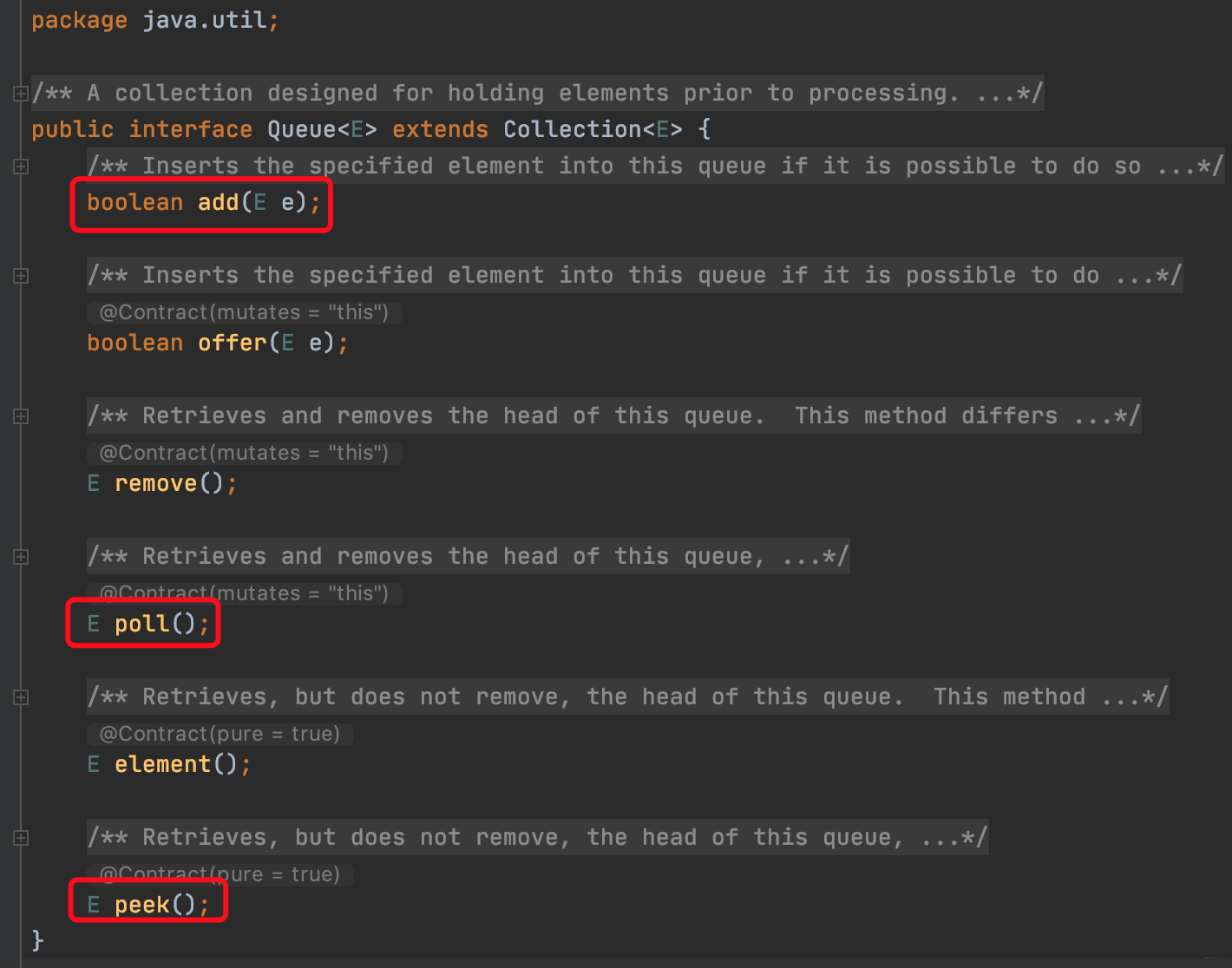
我们主要实现add、poll、和peek方法，并且会着重于算法的实现而不太着重一些细节的实现。

虽然优先队列和堆排序利用堆结构特性的流程有一些相似，但是两者其实还是有些操作上的区别的：

堆排序 ：

• 刚开始是一个杂乱无章的序列，所以需要将杂乱的序列（树）通过一个方法变成一个合法的堆。
• 转成一个堆之后需要删除n次每次删除完都要重新调整这个堆。没有插入操作。

优先队列：

• 队列（堆）刚开始的内容为空，每次增加一个元素时需要即使调整堆。每次删除也要及时调整堆，增加和删除每次都只是一个元素。

但是优先队列的具体操作流程是如何的呢？我们具体分析其插入和删除的流程。

插入add流程(小根堆为例)：

• 正常处理完的优先队列内的数据满足一个堆的结构，所以就是插入在堆中。
• 堆是一棵完全二叉树，所以在插入初始，插入到最后一个位置不影响其他结构。
• 节点和父节点比较大小(父节点索引为其二分之一)。如果该节点比父节点更小，则交换数据，一直到不能交换为止，这个过程不用担心不合法，因为父节点更小的话更满足比孩子节点更小。

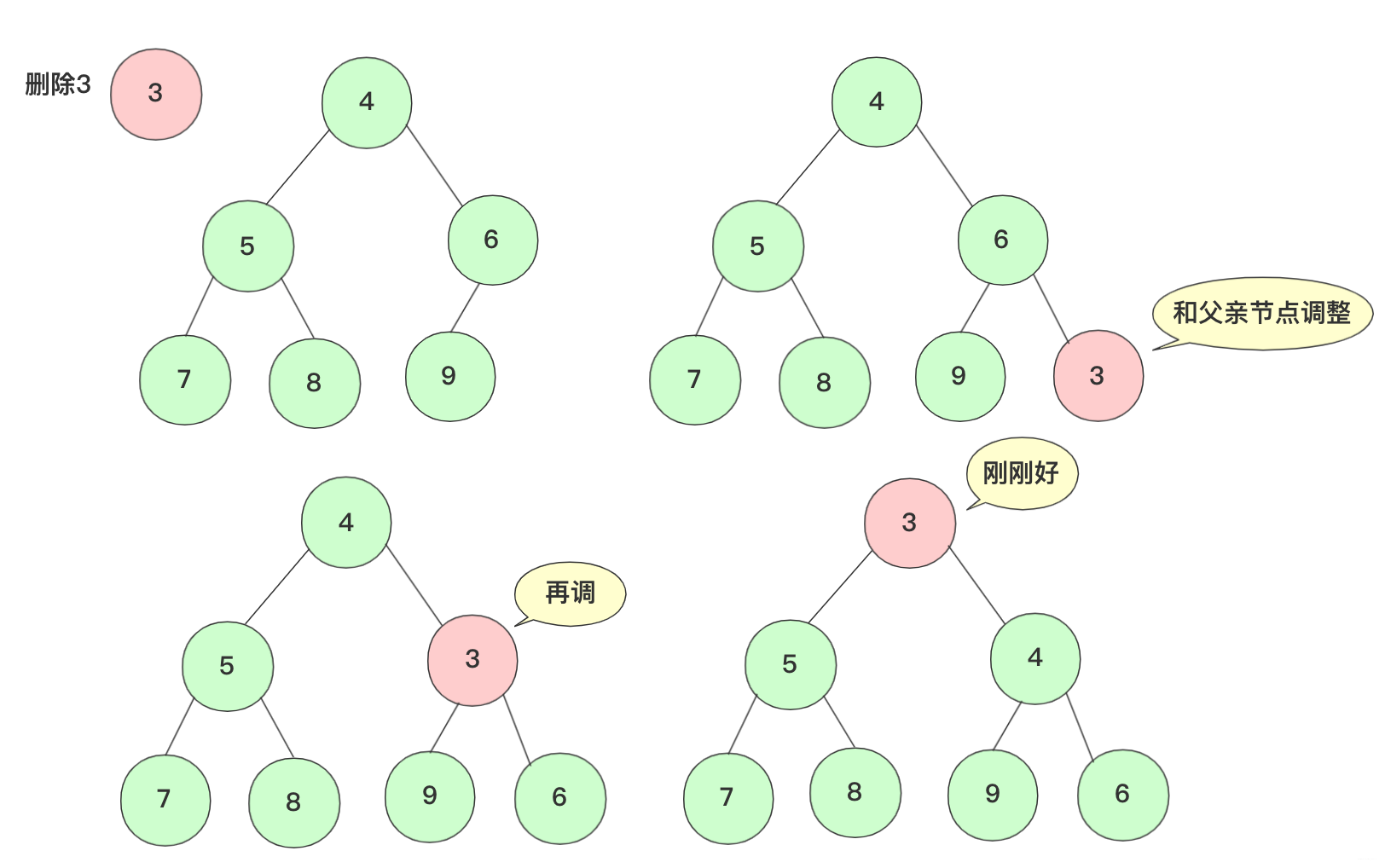
删除pop流程(小根堆为例)：

• pop删除操作取优先队列内最小的元素，而这个元素肯定就是堆顶元素了，取完之后，这个堆的其他部分还是满足堆的结构但是缺少堆顶。
• 为了不影响整个结构，我们将末尾的那个元素移到堆顶，此时堆需要调整使其满足堆的性质条件。
• 交换的这个节点和左右孩子进行比较，如果需要交换则交换，交换后再次考虑交换子节点是否需要交换，一直到不交换为止。最坏情况是交换到根节点，这个复杂度每次为O(logn).

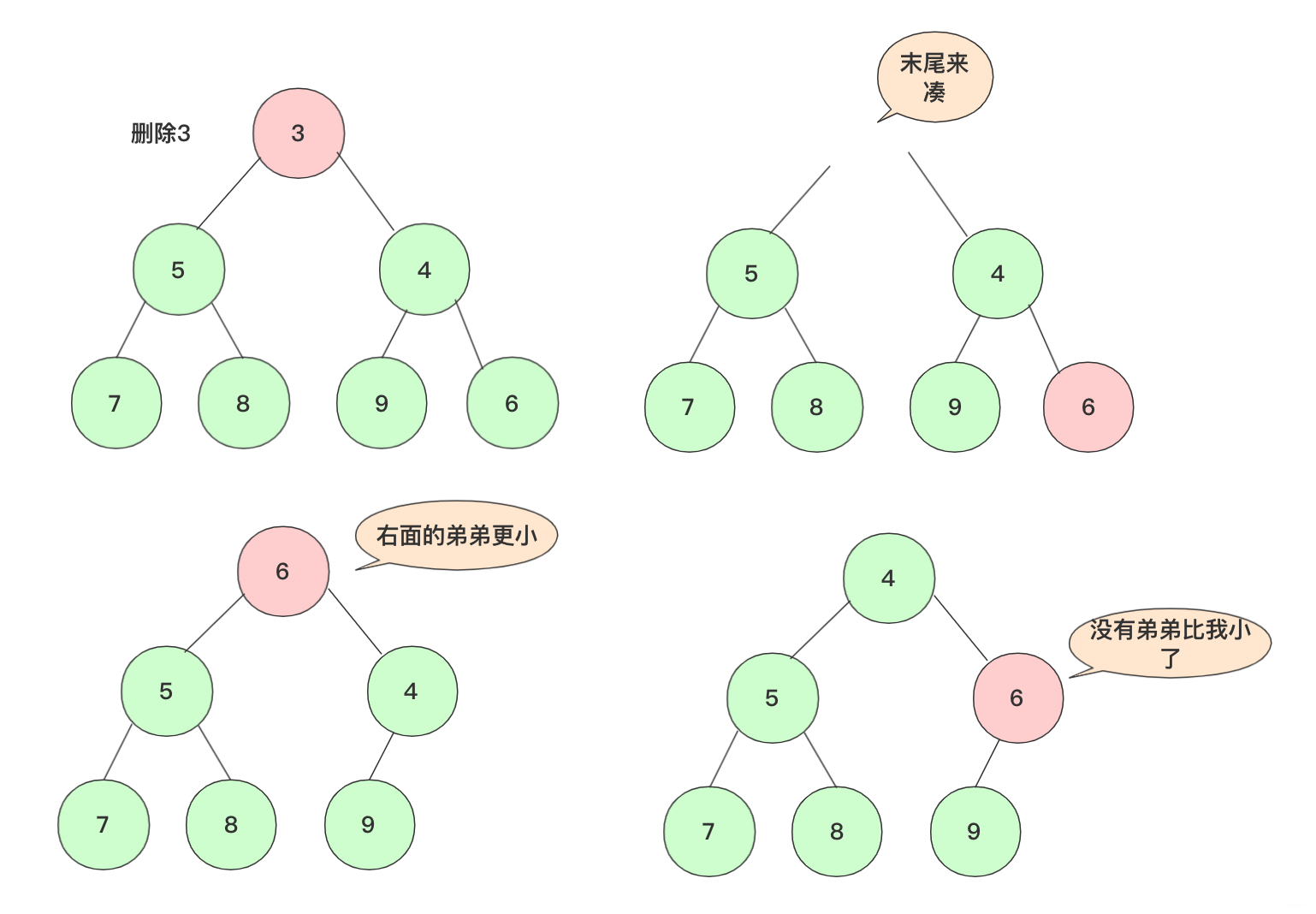
代码实现

我想到这里，优先队列的内部流程思想你已经掌握了，但是懂优先队列原理和手写优先队列是两个概念，为了更深入的学习优先队列，在这里就带你手写一个简易型的优先队列。

在代码的具体实现方面，最主要的就是pop()和add()两个函数了。在pop()函数具体实现的时候，将最后一个元素移到堆头考虑和其他孩子节点交换的时候，用while进行操作的时候计算孩子下标的时候要确保不越界。我们用的是数组存储数据，优先队列的长度不一定等于这个数组的长度。

而在实现add()函数的时候，这里简单的考虑了一下扩容。

具体实现的代码为：

import java.util.Arrays;

public class priQueue { private  int size;//优先队列的大小 private  int capacity;//数组的容量 private  int value[];//储存的值 public priQueue() { this.capacity = 10; this.value = new int[capacity]; this.size=0; } public priQueue(int capacity) { this.capacity = capacity; this.value = new int[capacity]; this.size=0; } /** * 插入元素 * @param number */ public void add(int number) { if(size==capacity)//扩容 { capacity*=1.5; value= Arrays.copyOf(value,capacity); } value[size++]=number;//先加到末尾 int index=size-1; while (index>=1) {//进行交换 if(value[index]<value[index/2]) { swap(index,index/2,value); index=index/2; } else//不需要交换即停止 break; } } public int peek() { return  value[0]; } /** * 抛出队头 * @return */ public int pop() { int val=value[0];//呆返回数据额 value[0]=value[--size];//将最后一个元素赋值在堆头 int index=0,leftChild=0,rightChild=0; while (true) { leftChild=index*2+1; rightChild=index*2+2; if(leftChild>=size)//左孩子必须满足在条件内 break; else if(rightChild<size&&value[rightChild]<value[index]&&value[rightChild]<value[leftChild]) {//右孩子更小 swap(index,rightChild,value); index=rightChild; } else if(value[leftChild]<value[index]) {//左孩子更小 swap(index,leftChild,value); index=leftChild; } else //不需要 它自己最小 break; } return  val; } //交换两个元素 public  void swap(int i,int j,int arr[]) { int team=arr[i]; arr[i]=arr[j]; arr[j]=team; } public int size() { return  size; }
}

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
  
55
  
56
  
57
  
58
  
59
  
60
  
61
  
62
  
63
  
64
  
65
  
66
  
67
  
68
  
69
  
70
  
71
  
72
  
73
  
74
  
75
  
76
  
77
  
78
  
79
  
80
  
81
  
82
  
83
  
84
 

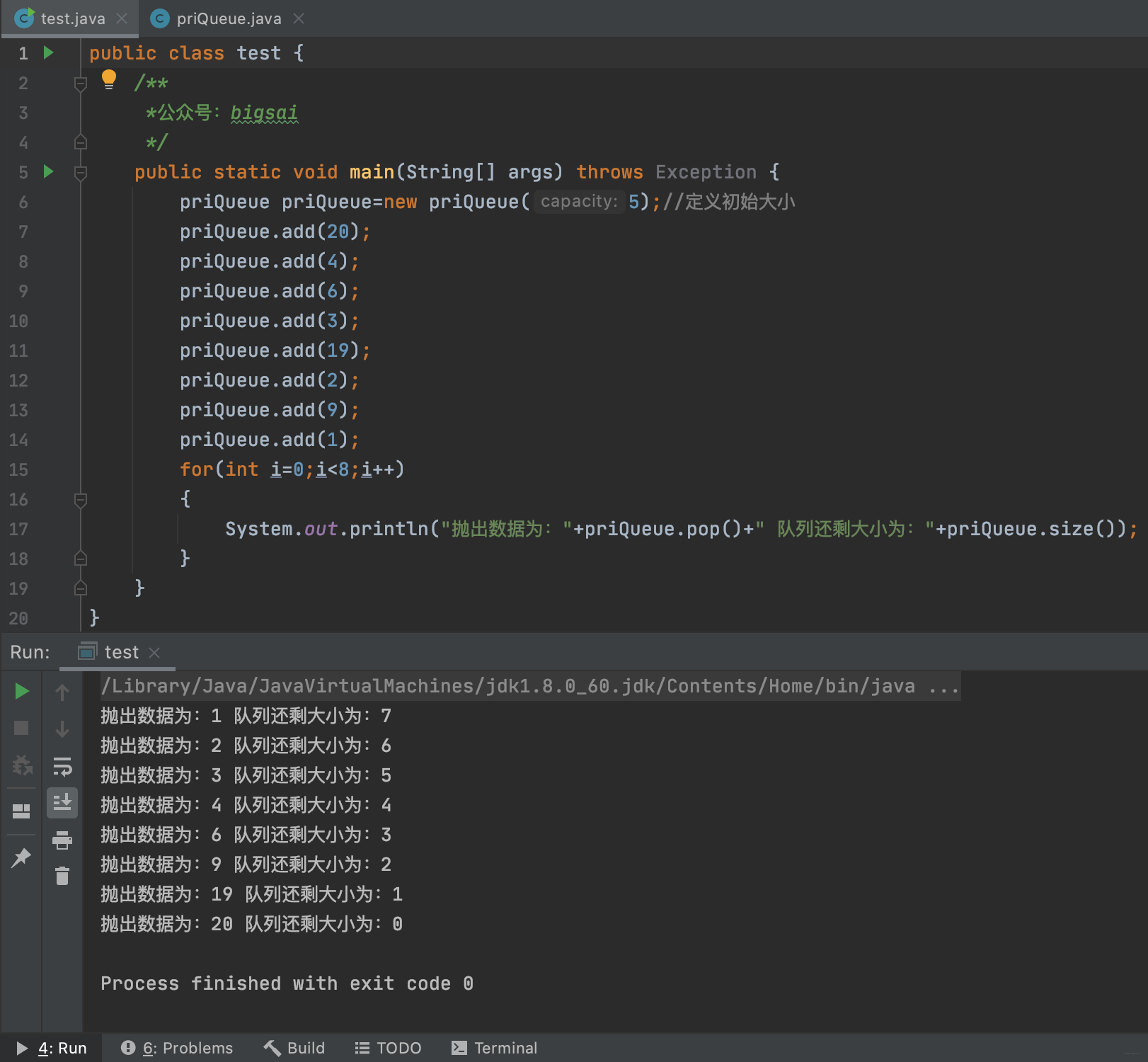
写个类测试一下看看：

结语

本次优先队列介绍就到这里啦，感觉不错记得点赞或一键三连哦，建议和堆排序一起看和学习效果更佳，要能够手写代码。个人公众号：bigsai 回复 bigsai 更多精彩和资源与你分享。

文章来源: bigsai.blog.csdn.net，作者：Big sai，版权归原作者所有，如需转载，请联系作者。

原文链接：bigsai.blog.csdn.net/article/details/109168876