面试官本拿求素数搞我,但被我优雅的“回击“了(素数筛)
原创公众号(希望能支持一下):bigsai 转载请联系bigsai
文章收录在github 求star
前言
现在的面试官,是无数开发者的梦魇,能够吊打面试官的属实不多,因为大部分面试官真的有那么那几下子。但在面试中,我们这些小生存者不能全盘否定只能单点突破—从某个问题上让面试官眼前一亮。这不,今天就来分享来了。
这年头,算法岗内卷不说,开发岗也有点内卷,对开发者要求越来越高了,而面试官也是处心积虑的 “刁难” 面试者,凡是都喜欢由浅入深,凡是都喜欢问个:你知道为什么?你知道原理吗?之类。并且,以前只是大厂面试官喜欢问算法,大厂员工底子好,很多甚至有ACM经验或者系统刷题经验,这很容易理解,但现在一些小公司面试官也是张口闭口 xx算法、xx数据结构你说说看,这不,真的被问到了。
求一个质数
在这么一次的过程,面试官问我算法题我不吃惊,我实现早把十大排序原理、复杂度分析、代码手写实现出来了,也把链表、树的各种操作温习的滚瓜烂熟,不过突然就是很诧异的面试官来了一道求素数问题,我把场景还原一下:
面试官:你知道怎么求素数吗?
我:求素数?
面试官:是的,就是求素数。
我:这很简单啊,判断一个数为素数,那么肯定就没有两个数(除了自身和1)相乘等于它,只需要枚举看看有没有能够被它整除的数就可以了,如果有那么就不是素数,如果没有,那么就是素数。
面试官露出一种失望的表情,说我说的对,但没答到点子上,让我具体说一下。
下面开始开始我的表演:
首先,最笨的方法,判断n是否为素数,就是枚举[2,n-1]之间有没有直接能够被n整除的,如果有,那么返回false这个就不是素数,否则就是素数,代码如下:
boolean isprime(int value){
for(int i=2;i<value;i++)
{ if(value%i==0) {return false;}
}
return true;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
这种判断一个素数的时间复杂度为O(n).
但是其实这种太浪费时间了,完全没必要这样,可以优化一下 。如果一个数不是质数,那么必定是两个数的乘积,而这两个数通常一个大一个小,并且小的小于等于根号n,大的大于等于根号n,我们只需要枚举小的可能范围,看看是否能够被整除,就可以判断这个数是否为素数啦。例如100=2*50=4*25=5*20=10*10 只需要找2—10这个区间即可。右侧的一定有个对应的不需要管它。
boolean isprime(int value)
{
for(int i=2;i*i<value+1;i++)
{ if(value%i==0) {return false;}
}
return true;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
这里之所以要小于value+1,就是要包含根号的情况,例如 3*3=9.要包含3.这种时间复杂度求单个数是O(sqrt(n))。面试官我给你画张图让你看看其中区别:
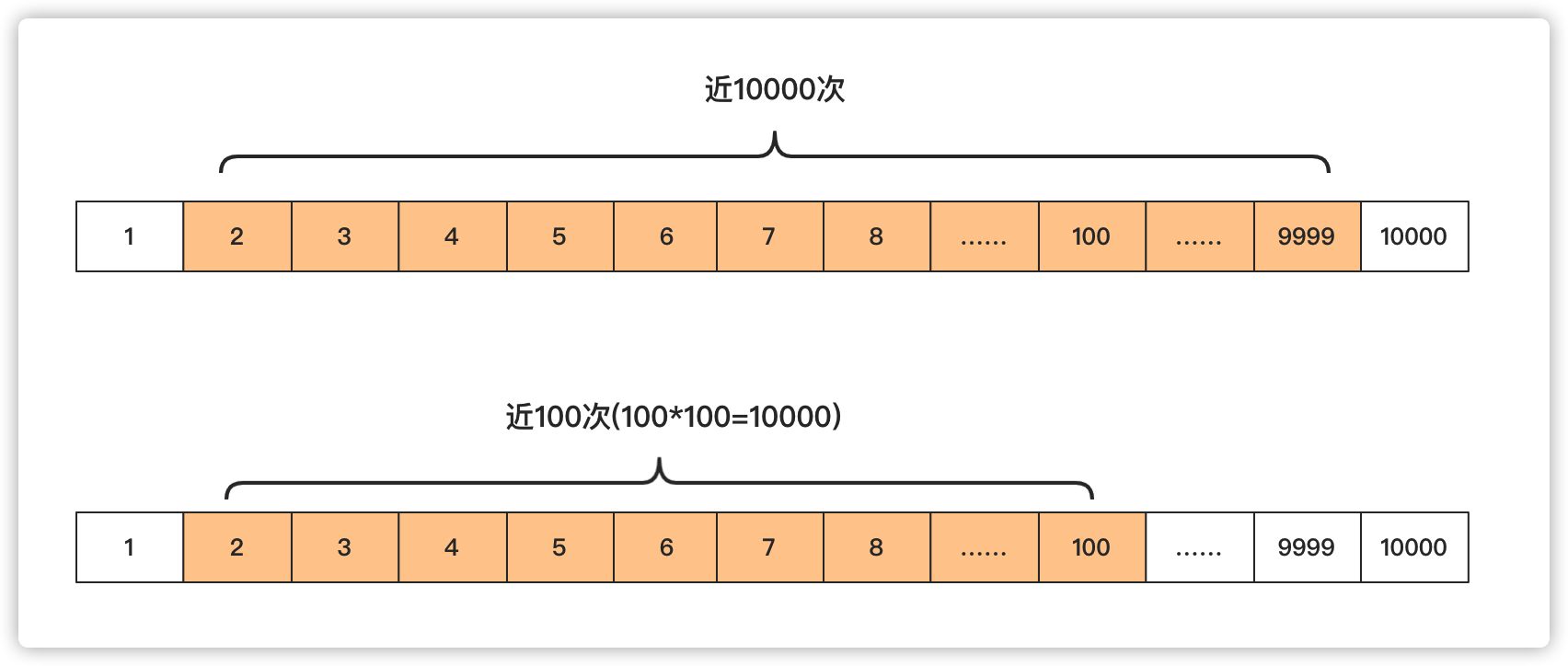
说到这里面试官露出欣慰的笑容。
面试官:不错不错,基本点掌握了
我:老哥,其实求素数精髓不在这,这个太低效在很多时候,比如求小于n的所有素数,你看看怎么搞?
面试官:用个数组用第二种方法求O(n*sqrt(n))还行啊。
求多个素数
求多个素数的时候(小于n的素数),上面的方法就很繁琐了,因为有大量重复计算,因为 计算某个数的倍数 是否为素数的时候出现大量的重复计算,如果这个数比较大那么对空间浪费比较多。
这样,素数筛的概念就被发明和使用。筛的原理是从前往后进行一种递推、过滤排序以来统计素数。
埃拉托斯特尼(Eratosthenes)筛法
我们看一个数如果不是为素数,那么这个数没有数的乘积能为它,那么这样我们可以根据这个思想进行操作啊:
直接从前往后枚举,这个数位置没被标记的肯定就是素数,如果这个数是素数那么将这个数的倍数标记一下(下次遍历到就不需要在计算)。如果不是素数那么就进行下一步。这样数值越大后面计算次数越少,在进行具体操作时候可借助数组进行判断。所以埃氏筛的核心思想就是将素数的倍数确定为合数。
假设刚开始全是素数,2为素数,那么2的倍数均不是素数;然后遍历到3,3的倍数标记一下;下个是5(因为4已经被标记过);一直到n-1为止。具体流程可以看图:
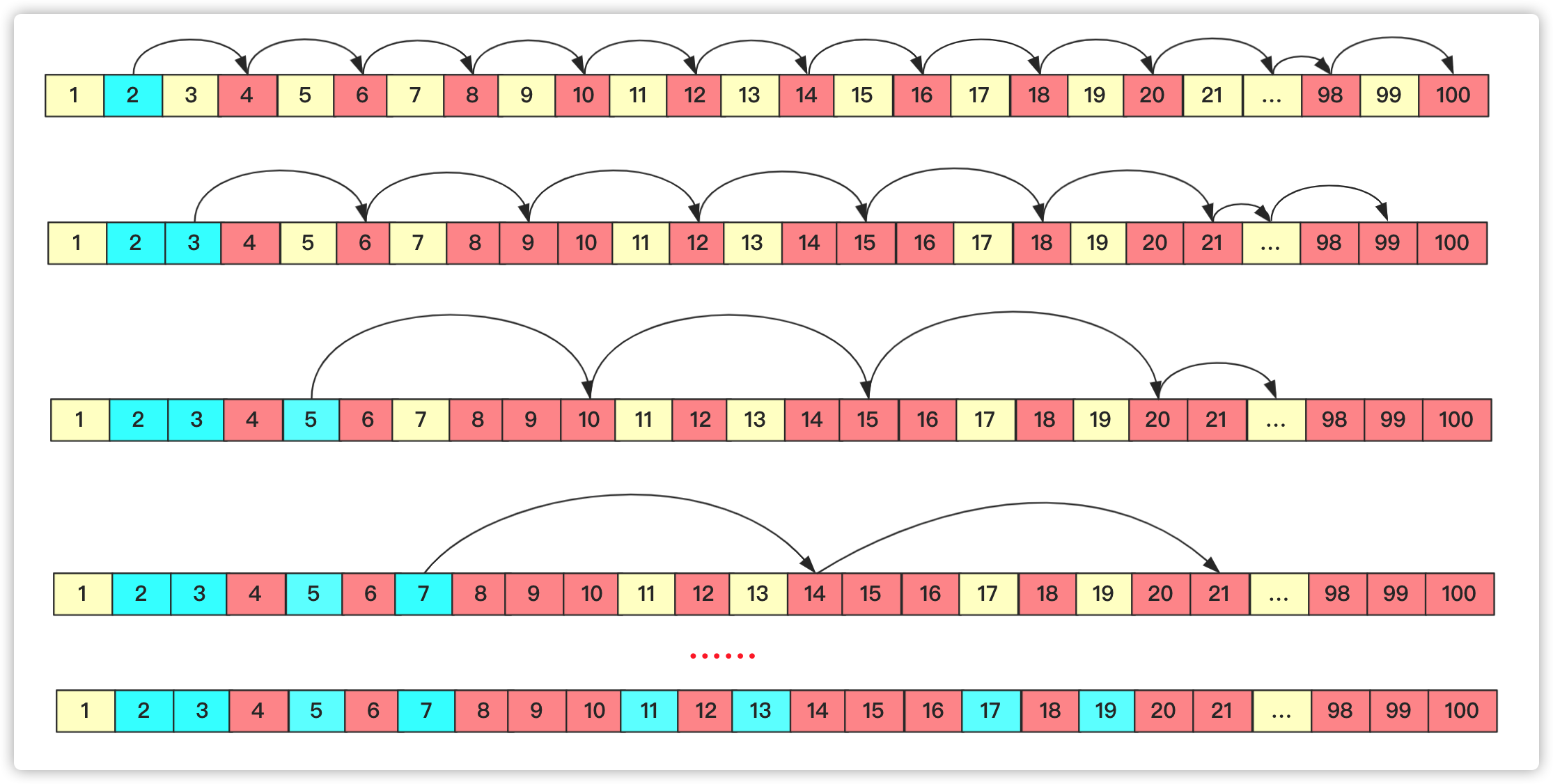
具体代码为:
boolean isprime[];
long prime[];
void getprime()
{
prime=new long[100001];//记录第几个prime int index=0;//标记prime当前下标
isprime=new boolean [1000001];//判断是否被标记过
for(int i=2;i<1000001;i++)
{ if(!isprime[i]) { prime[index++]=i; } for(int j=i+i;j<1000000;j=j+i)//他的所有倍数都over { isprime[j]=true; }
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
这种筛的算法复杂度为O(nloglogn);别小瞧多的这个logn,数据量大一个log可能少不少个0,那时间也是十倍百倍甚至更多的差距。
欧拉筛
面试官已经开始点头赞同了,哦哦的叫了起来,可其实还没完。还有个线性筛—欧拉筛。观察上述的埃氏筛,有很多重复的计算,尤其是前面的素数,比如2和3的最小公倍数为6,每3次2的计算就也会遇到是3的倍数,而欧拉筛在埃氏筛的基础上改进,有效的避免了这个重复计算。
具体是何种思路呢?就是埃氏筛是遇到一个质数将它的倍数计算到底,而欧拉筛则是只用它乘以已知晓的素数的乘积进行标记,如果素数能够被整除那就停止往后标记。
在实现上同样也是用两个数组,一个存储真实有效的素数,一个用来作为标记使用。
- 在遍历到一个数的时候,如果这个数没被标记,那么这个数存在素数的数组中,对应下标加1.
- 不管这个数是不是素数,遍历已知素数将它和该素数的乘积值标记,如果这个素数能够被当前值i整除,那么停止操作进行下一轮。
具体实现的代码为:
boolean isprime[];
int prime[];
void getprimeoula()// 欧拉筛
{
prime = new int[100001];// 记录第几个prime
int index = 0;
isprime = new boolean[1000001];
for (int i = 2; i < 1000001; i++) { if (!isprime[i]) { prime[index++] = i; } for (int j = 0; j < index && i * prime[j] <= 100000; j++){//已知素数范围内枚举 isprime[i * prime[j]] = true;// 标记乘积 if (i % prime[j] == 0) break; }
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
你可能会问为啥if (i % prime[j] == 0)就要break。
如果i%prime[j]==0,那么就说明i=prime[j]*k. k为一个整数。
那么如果进行下一轮的话
i*prime[j+1]=(prime[j]*k)*prime[j+1]=prime[j]*(k*prime[j+1]) 当i=k*prime[j+1]两个位置就产生冲突重复计算啦,所以一旦遇到能够被整除的就停止。
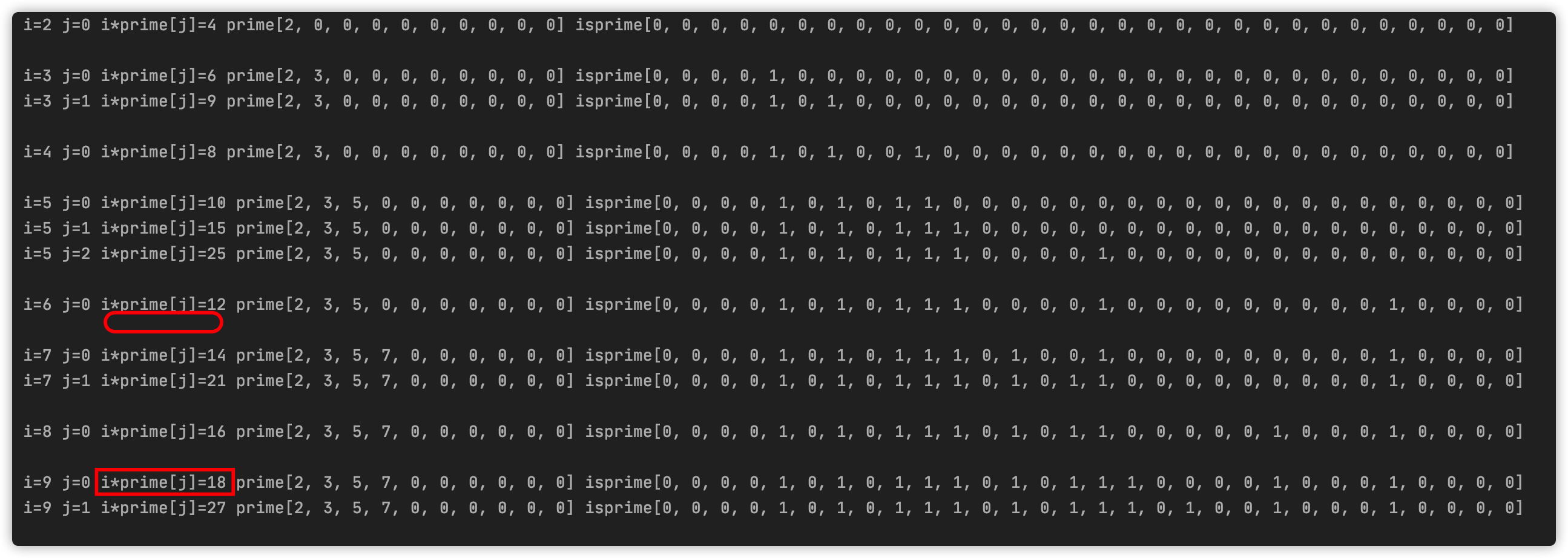
你可以看到这个过程,6只标记12而不标记18,18被9*2标记。详细理解还需要多看看代码想想。过程图就不画啦!欧拉的思路就是离我较近的我给它标记。欧拉筛的时间复杂度为O(n),因为每个数只标记一次。
面试官露出一脸欣赏的表情,说了句不错,下面就是聊聊家常,让我等待下一次面试!

原创不易,bigsai我请你帮两件事帮忙一下:
-
点赞支持一下, 您的肯定是我在csdn创作的源源动力。
-
微信搜索「bigsai」,关注我的公众号(新人求支持),不仅免费送你电子书,我还会第一时间在公众号分享知识技术。加我还可拉你进力扣打卡群一起打卡LeetCode。
记得关注、咱们下次再见!

文章来源: bigsai.blog.csdn.net,作者:Big sai,版权归原作者所有,如需转载,请联系作者。
原文链接:bigsai.blog.csdn.net/article/details/111027378
- 点赞
- 收藏
- 关注作者


评论(0)