程序员必备数据结构:堆

前言
自从写完了上一篇:程序员必备数据结构:栈之后,就一直盘算着写一篇“堆”,今天动手了。
堆,是什么?
二叉堆是完全二叉树或者是近似完全二叉树。
二叉堆满足二个特性:
1.父结点的键值总是大于或等于(小于或等于)任何一个子节点的键值。
2.每个结点的左子树和右子树都是一个二叉堆(都是最大堆或最小堆)。
当父结点的键值总是大于或等于任何一个子节点的键值时为最大堆。当父结点的键值总是小于或等于任何一个子节点的键值时为最小堆。
下图用一个数组来表示堆:
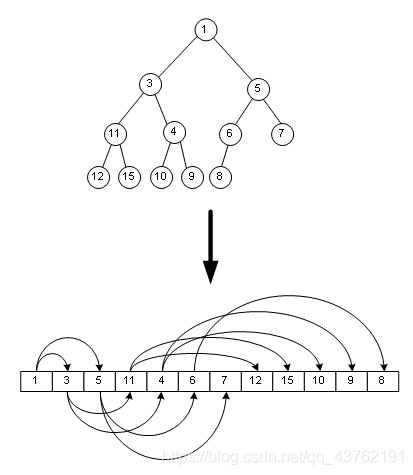
由于其它几种堆(二项式堆,斐波纳契堆等)用的较少,一般将二叉堆就简称为堆。
二叉堆的应用
奈何我比较笨,网上五花八门的介绍,我就看出来三个字:堆排序。关于堆的一切应用,也都是基于堆排序的基础上衍生的,所以,本篇不废话,就围绕堆排序展开。
堆的插入
别问我怎么建堆,看完插入,自己去想,反正不是先排序,再建堆。
先看个图:
假设要在这个二叉堆里入队一个单元,键值为2,那么只需在数组末尾加入这个元素,然后尽可能把这个元素往上移动,直到挪不动,经过了这种复杂度O(logn)的操作,二叉堆还是二叉堆。
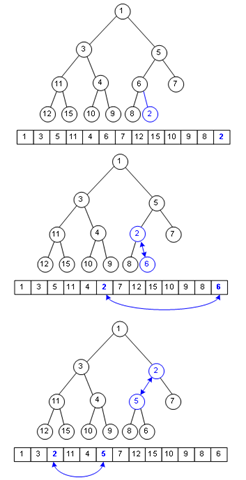
代码实现
#include<iostream>
#include<vector>
using namespace std;
void push_heap(vector<int>& vec, int num) {
vec.push_back(num);
int sz = vec.size()-1;
int parent = sz / 2 - 1;
while (vec[sz] < vec[parent]) { vec[sz] ^= vec[parent];
vec[parent] ^= vec[sz];
vec[sz] ^= vec[parent]; sz = parent;
parent /= 2;
}
}
int main() {
vector<int> vec = {1,3,5,11,4,6,7,12,15,10,9,8};
push_heap(vec,2);
for (int i = 0; i < 13; i++) {
cout << vec[i]<<" ";
}
cout << endl;
return 0;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
重新看这篇文章
在往下看之前,请诸君自行实现上面那个堆的插入与调整,因为我们接下来要进入源码了。
源码之前,了无秘密
向下调整算法
向下调整算法的说明:
*要建一个大堆,即最后每一个堆的节点的值都大于它的孩子
*我们先找左右孩子中最大的一个
*然后让最大的一个孩子和父节点进行比较:
如果孩子大于父节点的值,那么进行交换,并将孩子的值赋给父节点,孩子的值也随父节点的值变化,否则就结束。
*进行向下调整是从根节点开始的,因此,最终的大循环是孩子的值要小于数组存储的元素的值
代码实现(大堆)
//建堆
//建堆所用数组:vector<T> _a
Heap(T* a, size_t n)
:_a(a,a+n)
{
for(int i = (_a.size()-2)/2; i>=0; i--)
{ _Adjustdown(i);
}
}
//向下调整
void _Adjustdown(int root)
{
int parent = root;
int child = parent*2+1;
//此处的条件有两个:
//一个是当孩子的值小于父母的值时候这个已经在break处理过了
//第二个条件就是当是叶子节点的时候
while(child<_a.size())
{ //找左右孩子中值最大的 if(child+1<_a.size() && _a[child+1]>_a[child]) { ++child; } //将孩子和父母做比较 if(_a[child]>_a[parent]) { swap(_a[child],_a[parent]); parent = child; child = parent*2+1; } else { break; }
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
向上调整算法
和向下调整算法很相似
*直接让孩子和父节点进行比较
如果孩子比父节点大的话,就将父亲赋给孩子,然后父亲的值进行改变,一直向上调整,否则结束
*调整结束的另一个结束条件是当调整到最上面的堆顶的时候结束,即就是孩子的值<0
上面那个尾插算法就是个向上调整的。
代码实现(大堆)
//尾插
void Push(const T& x)
{
_a.push_back(x);
_Adjustup(_a.size()-1);
}
//向上调整
void _Adjustup(int i)
{
int child = i;
int parent = (i-1)/2;
while(child >= 0)
{ if(_a[child] > _a[parent]) { swap(_a[child],_a[parent]); child = parent; parent = (parent-1)/2; } else { break; }
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
堆顶元素删除
*先将要删除的堆顶的元素和最后一个元素进行交换
*然后删除尾部的元素
*再进行向下调整
代码实现
//尾删
void Pop()
{
swap(_a[0],_a[_a.size()-1]);
_a.pop_back();
_Adjustdown(0);
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
堆排序(大堆)
*如果我们是升序的话,要建大堆
*将第一个元素和最后一个元素进行交换,然后进行向下调整
*然后循环第二步,知道堆里剩一个元素,结束
代码实现
#include<iostream>
#include<vector>
using namespace std;
template<typename T>
class Heap
{
public:
//构造函数
Heap()
{}
//建堆
Heap(T* a, size_t n)
:_a(a,a+n)
{
for(int i = (_a.size()-2)/2; i>=0; i--)
{ _Adjustdown(i);
}
} //堆排
void HeapSort()
{
//升序,建大堆
for(int i = (_a.size()-2)/2; i>=0; --i)
{ _Adjustdown(i);
}
int end = _a.size()-1;
while(end>0)
{ swap(_a[0],_a[_a.size()-1]); _Adjustdown(end); --end;
}
}
protected:
//向下调整
void _Adjustdown(int root)
{
int parent = root;
int child = parent*2+1;
//此处的条件有两个:
//一个是当孩子的值小于父母的值时候这个已经在break处理过了
//第二个条件就是当是叶子节点的时候
while(child<_a.size())
{ //找左右孩子中值最大的 if(child+1<_a.size() && _a[child+1]>_a[child]) { ++child; } //将孩子和父母做比较 if(_a[child]>_a[parent]) { swap(_a[child],_a[parent]); parent = child; child = parent*2+1; } else { break; }
}
}
//向上调整
void _Adjustup(int i)
{
int child = i;
int parent = (i-1)/2;
while(child >= 0)
{ if(_a[child] > _a[parent]) { swap(_a[child],_a[parent]); child = parent; parent = (parent-1)/2; } else { break; }
}
}
protected:
vector<T> _a;
};
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
文章来源: lion-wu.blog.csdn.net,作者:看,未来,版权归原作者所有,如需转载,请联系作者。
原文链接:lion-wu.blog.csdn.net/article/details/107340521
- 点赞
- 收藏
- 关注作者


评论(0)