走进STL - 红黑树,是圣诞树吗
如果对树的基础不牢固的话,请先移步:拥抱STL - 树的导览(AVL-tree)
如果后面发现看不懂了,也可以划上来看看。
我的STL专栏 是一个系列,所以代码中特定的名词不理解可以去之前的文章看看
1、红黑树?长什么果实吗
红黑树,又称RB-tree,是一种平衡二叉搜索树。不过它这个平衡没有AVL-tree要求那么严格罢了。(最长路径不超过最短路径的两倍)
红黑树的规矩:
- 每个节点,非黑即红。
- 根节点为黑。
- 不能存在连续的两个红节点。
- 任何节点,至其下属的、不同的叶节点的每条路径上,黑节点数必须相等。
好,看了上面这些规矩,你是不是在想:这什么SJ病的规矩,这还是人能弄出来的吗?
没错,我就是这样想的,这样想很正常。确实绕。
稍微来看一下这几个规则。
首先规则四便锁死了新增节点,妥妥得是红节点。
然而规则三又锁定了叶节点的父节点为黑节点。
那就涉及到一个问题:如果某叶节点为红,要再它后面新增节点,怎么办?
那就只有调整颜色并旋转树形。
这个调整的时候,可不能忘了它是红黑树,还是平衡二叉树,更是搜索树。所以还得守平衡二叉搜索树的规矩。
2、红黑树的节点设计
typedef bool __rb_tree_color_type;
const __rb_tree_color_type __rbtree_red = false; //红0
const __rb_tree_color_type __rbtree_black = true; //黑1
struct __rb_tree_node_base
{
typedef __rb_tree_color_type color_type;
typedef __rb_tree_node_base* base_ptr;
color_type color;
base_ptr parent;
base_ptr left;
base_ptr right;
static base_ptr minimum(base_ptr x)
{ ··· }
static base_ptr maximum(base_ptr x)
{ ··· }
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
template <class Value>
struct __rb_tree_node :public __rb_tree_node_base
{
typedef ____rb_tree_node<Value>* link_type;
Value value_field; //节点值
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
3、 红黑树的数据结构
红黑树每次配置一个节点的空间。
template<class Key,class Value,class KeyOfValue,class Compare,class Alloc = alloc>
class rb_tree
{
protected:
typedef void* void_pointer;
typedef __rb_tree_node<Value> rb_tree_node;
typedef __rb_tree_node* base_ptr;
typedef simple_alloc<rb_tree_node,Alloc> rb_tree_node_allocator;
typedef __rb_tree_color_type color_type;
public:
typedef Key key_type;
typedef Value value_type;
typedef value_type* pointer;
typedef const value_type* const_pointer;
typedef value_type& reference;
typedef rb_tree_node* link_node;
typedef size_t size_type;
typedef ptrdiff_t difference_type;
protected:
··· link_type header; //这是实现上的一个技巧
Compare key_compare; //节点间的键值大小比较准则 //以下三个函数用于取得header的成员
link_type& root() const { return (link_type&)header->parent; }
link_type& leftmost() const { return (link_type&)header->left; }
link_type& rightmost() const { return (link_type&)header->right; }
···
};
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
红黑树的构造有两种,一种是显式定义的复制构造函数,另一种是一颗空树。
4、红黑树插入节点
4.1 元素插入操作(insert_equal())
允许节点键值相同
//返回的是一个RB-tree迭代器,指向新增节点
template<class Key,class Value,class KeyOfValue,class Compare,class Alloc>
typename rb_tree<Key,Value,KeyOfValue,Compare,Alloc>::iterator // 这一行是返回值类型
rb_tree<Key,Value,KeyOfValue,Compare,Alloc>::insert_equal(const Value& v) //这句看不懂的话我还有另一篇博客专门讲解这种句法,只是代码块里面放不了链接
{
link_type y = header;
link_type x = root();
while(x!=0)
{
y = x;
x = key_compare(KeyOfValue()(v),key(x)) ? left(x) : right(x); //左右转
}
return __insert(x,y,v); //x:新值插入点 y:插入点之父节点 v:新值
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
4.2 元素插入操作(insert_unique())
插入新值,节点键值不允许重复,若重复则插入无效
template<class Key,class Value,class KeyOfValue,class Compare,class Alloc>
pair<typename rb_tree<Key,Value,KeyOfValue,Compare,Alloc>::iterator> // 这一行是返回值类型
rb_tree<Key,Value,KeyOfValue,Compare,Alloc>::insert_unique(const Value& v)
{
link_type y = header;
link_type x = root();
bool comp = true;
while( x != 0 )
{
y = x;
comp = key_compare(KeyOfValue()(v),key(x)); x = comp ? left(x) : right(x); //左右转
}
//循环转出来之后,y所指的便是插入节点的父节点,此时y必为叶节点
iterator j = iterator(y); //令迭代器j指向插入y
if(comp) //y节点值大于新值
if(j == begin()) //如果插入点的父节点为最左 return pair<iterator,bool>(__insert(x,y,v),true);
else --j; //调整j,回头准备测试(我也不知道要测试啥)
if(key_compare(key(j.node)KeyOfValue(key())(v)) //y节点小于新值
return pair<iterator,bool>(__insert(x,y,v),true);
return pair<iterator,bool>(j,false);//要是走到这一步,那说明键值重复了
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
4.3 插入的幕后黑手(__insert())
template<class Key,class Value,class KeyOfValue,class Compare,class Alloc>
typename rb_tree<Key,Value,KeyOfValue,Compare,Alloc>::iterator // 这一行是返回值类型
rb_tree<Key,Value,KeyOfValue,Compare,Alloc>::__insert(base_ptr x_,base_ptr y_,const Value& v)
{
link_type y = link_type y_;
link_type x = link_type x_;
link_type z;
if(y == header || x!=0 || Key_compare(KeyOfValue()(v),key(y)))
{
z = create_node(v); //产生一个新节点
left(y) = z;
if(y == header)
{ root() = z; rightmost() = z;
}
else if(y == leftmost()) leftmost() = z;
}
else
{
z = create_node(v);
right(y) = z;
if(y == rightmost()) rightmost() = z;
}
parent(z) = y; //设定新节点的父节点
left(z) = 0;
right(z) = 0;
__rb_tree_rebalalance(z,header->parent);
++node_count;
return iterator(z); //返回一个迭代器,指向新节点
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
5、调整红黑树
5.1 旋转与改变颜色
任何插入操作,在插入完成之后,都需要做一次调整性操作,将树的状态调整到符合RB-tree的要求。
//函数功能:重新令树型平衡
inline void __rb_tree_rebalance(__rb_tree_node_base* x/* 新增节点*/,__rb_tree_node_base*& root)
{
x->color = __rb_tree_red;
while( x != root && x->parent->color == __rb_tree_red) //父节点为红
{
if( x->parent == x->parent->parent->left ) //父节点为祖父节点的左子节点
{ __rb_tree_node_base* y = x->parent->parent->right; //将y作为它的伯父节点 if( y && y->color == __rb_tree_red) //如果真的有伯父节点,且为红 { x->parent->color = __rb_tree_black; //将父节点改黑 y->color = __rb_tree_black; //将伯父也抹黑 y->parent->color = __rb_tree_red; //把爷爷放红 x = x->parent->parent; //自己当爷爷 } else //没有伯父,或者伯父是非洲回来的 { if( x == x->parent->right) //如果新节点为父节点右孩子 { x = x->parent; //自己当爸爸 __rb_tree_rotate_left(x,root); //第一参数为左旋点 } x->parent->color = __rb_tree_black; //将父节点抹黑 x->parent->parent->color = __rb_tree_red; //把爷爷放红 __rb_tree_rotate_right(x->parent->parent,root); //第一参数为右旋点 }
} else //父节点为祖父节点右子节点
{ __rb_tree_node_base* y = x->parent->parent->left; //令y为伯父节点 if( y && y->color == __rb_tree_red) //如果真的有伯父节点,且为红 { x->parent->color = __rb_tree_black; //将父节点改黑 y->color = __rb_tree_black; //将伯父也抹黑 y->parent->color = __rb_tree_red; //把爷爷放红 x = x->parent->parent; //自己当爷爷 } else //没有伯父,或者伯父是非洲回来的 { if( x == x->parent->left) //如果新节点为父节点左孩子 { x = x->parent; //自己当爸爸 __rb_tree_rotate_right(x,root); //第一参数为左旋点 } x->parent->color = __rb_tree_black; //将父节点抹黑 x->parent->parent->color = __rb_tree_red; //把爷爷放红 __rb_tree_rotate_right(x->parent->parent,root); //第一参数为右旋点 }
}
} //while结束
root->color = __rb_tree_black; //根节点抹黑
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
//源码之前,了无秘密。
操作流程图稍后会画。
//左旋
inline void __rb_tree_rotate_left(__rb_tree_node_base* x,__rb_tree_node_base*& root)
{
__rb_tree_node_base* y = x->right; //令y为旋转点的右子节点
x->right = y->left; //令旋转点的右子节点的左子节点为旋转点的右节点
if(y->left != 0)
y->left->parent = x; //并不知道这个有什么意义
y->parent = x->parent;
//令y完全顶替x的位置
if(x == root)
root = y;
else if(x == x->parent->left)
x->parent->left = y;
else
x->parent->right = y;
y->left = x;
x->parent = y;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
//右旋
inline void __rb_tree_rotate_right(__rb_tree_node_base* x,__rb_tree_node_base*& root)
{
__rb_tree_node_base* y = x->left; //令y为旋转点的左子节点
x->left = y->right; //令旋转点的右子节点的左子节点为旋转点的右节点
if(y->right != 0)
y->right->parent = x; //并不知道这个有什么意义
y->parent = x->parent;
//令y完全顶替x的位置
if(x == root)
root = y;
else if(x == x->parent->right)
x->parent->right = y;
else
x->parent->left = y;
y->right = x;
x->parent = y;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
6、红黑树工作流程图
前面都是不说两句就贴代码,接下来就比较友好了,贴图。
话说,源码之前,了无秘密。但是就算备注给你了,看着还费劲呢。
所以,我便想重源码之中整理处一份流程图,留待有缘人。CSDn上搜红黑树,一搜一大把,但是既然打开了我的,看了这么多,那我就得留点彩蛋才是》
先来张红黑树的流程图:
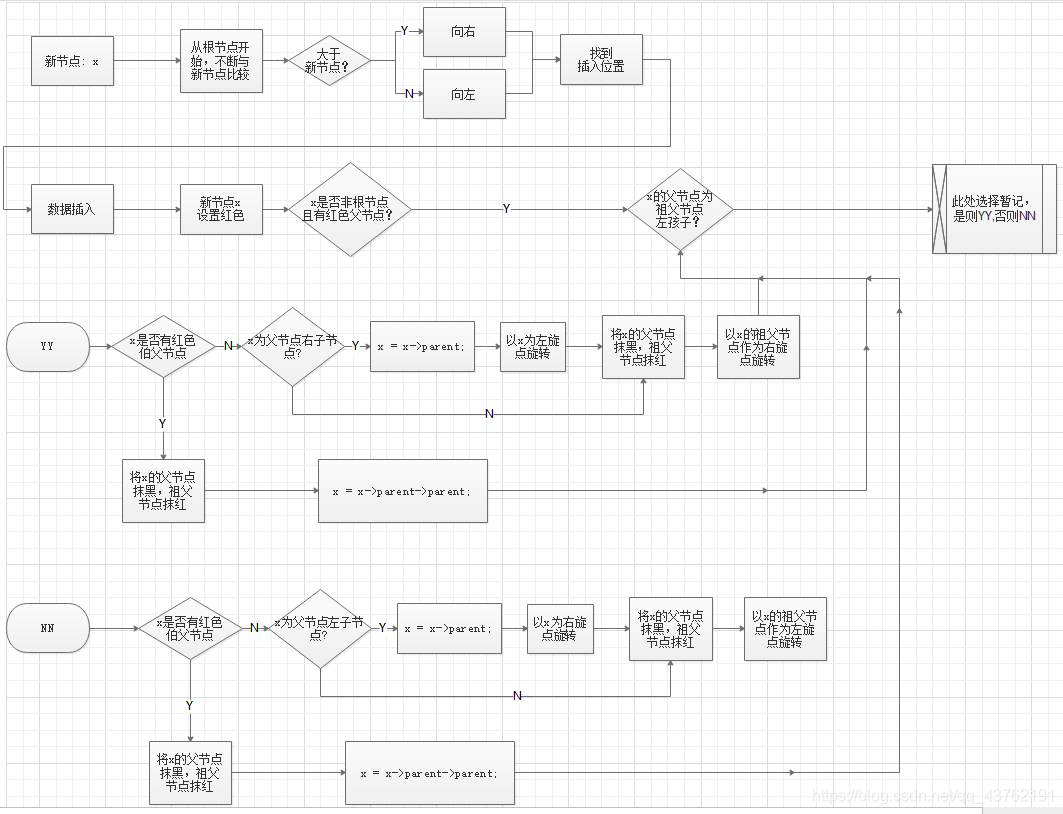
7、红黑树图示
由于时间关系这里没配上操作图了,
其实是我发现另一篇的图实在太精美了,让我不好意思画了。
这里给出链接:漫画图解 - 红黑树
文章来源: lion-wu.blog.csdn.net,作者:看,未来,版权归原作者所有,如需转载,请联系作者。
原文链接:lion-wu.blog.csdn.net/article/details/105536650
- 点赞
- 收藏
- 关注作者


评论(0)