LeetCode精选好题(二)
选进来的,都是我二刷之后确定我自己会做的。
9、二叉树的最大深度
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
代码实现:
int maxDepth(TreeNode* root) {
if(root == NULL) return 0;
return 1 + max(maxDepth(root->left), maxDepth(root->right));
}
- 1
- 2
- 3
- 4
- 5
10、对称二叉树
原来递归的空间复杂度也是O(n),我还以为递归没有空间消耗。
给定一个二叉树,检查它是否是镜像对称的。
例如,二叉树 [1,2,2,3,4,4,3] 是对称的。
1 / \
2 2
/ \ / \
3 4 4 3
- 1
- 2
- 3
- 4
- 5
但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:
1 / \
2 2 \ \ 3 3
- 1
- 2
- 3
- 4
- 5
迭代思路:
中序遍历,将值取出放到容器中,然后对容器进行操作。
class Solution {
public: bool check(TreeNode *u, TreeNode *v) { queue <TreeNode*> q; q.push(u); q.push(v); while (!q.empty()) { u = q.front(); q.pop(); v = q.front(); q.pop(); if (!u && !v) continue; if ((!u || !v) || (u->val != v->val)) return false; q.push(u->left); q.push(v->right); q.push(u->right); q.push(v->left); } return true; } bool isSymmetric(TreeNode* root) { return check(root, root); }
};
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
时间复杂度:O(n)。
空间复杂度:这里需要用一个队列来维护节点,每个节点最多进队一次,出队一次,队列中最多不会超过 n 个点,故渐进空间复杂度为 O(n)
12、二叉树的层序遍历
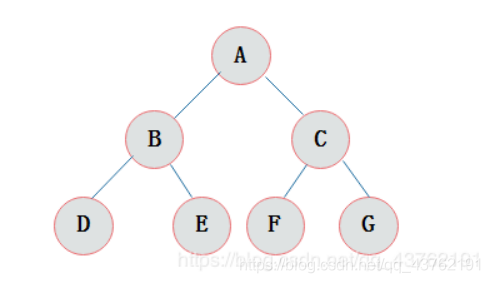
1.创建队列,存储每一层的结点;
2.使用循环从队列中弹出一个结点:
2.1获取当前结点的key;
2.2如果当前结点的左子结点不为空,则把左子结点放入到队列中
2.3如果当前结点的右子结点不为空,则把右子结点放入到队列中
这让我很吃惊,我居然是个会用栈的人,我一直以为自己只知道用vector。。。
代码实现:
#include<queue>
#include<iostream>
using namespace std;、
void LevelOrder(Node *root) {
if (root == NULL)
return;
queue<Node *> q;
// 启动
q.push(root);
while (!q.empty()) {
Node *front = q.front();
q.pop();
cout<<front->value;
if (front->left != NULL) q.push(front->left);
if (front->right != NULL) q.push(front->right);
}
cout<<endl;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
13、将有序数组转换为二叉搜索树
将一个按照升序排列的有序数组,转换为一棵高度平衡二叉搜索树。
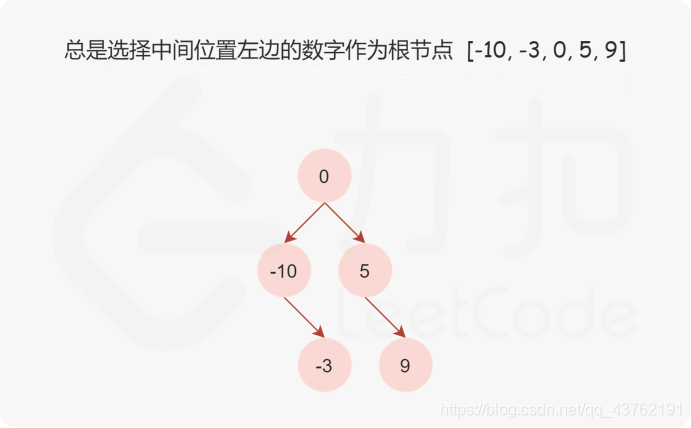
思路:
其实思路很直接的,二分法。
选择中间位置左边的数字作为根节点,则根节点的下标为 mid=(left+right)/2,此处的除法为整数除法。
代码实现:
class Solution {
public: TreeNode* sortedArrayToBST(vector<int>& nums) { return helper(nums, 0, nums.size() - 1); } TreeNode* helper(vector<int>& nums, int left, int right) { if (left > right) return NULL; // 总是选择中间位置左边的数字作为根节点 int mid = (left + right) / 2; TreeNode* root = new TreeNode(nums[mid]); root->left = helper(nums, left, mid - 1); root->right = helper(nums, mid + 1, right); return root; }
};
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
14、爬楼梯
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
注意:给定 n 是一个正整数。
示例 1:
输入: 2
输出: 2
- 1
- 2
- 3
解释: 有两种方法可以爬到楼顶。
- 1 阶 + 1 阶
- 2 阶
示例 2:
输入: 3
输出: 3
- 1
- 2
- 3
解释: 有三种方法可以爬到楼顶。
- 1 阶 + 1 阶 + 1 阶
- 1 阶 + 2 阶
- 2 阶 + 1 阶
思路:
n阶 = (n-1)阶+(n-2)阶
但是自顶向下递归会导致超时,也确实,因为n一旦大起来,递归使用的栈空间和时间将是巨大的。所以采用自底向上的斐波那契数列法。
代码实现:
int climbStairs(int n) { if(n == 1) return 1; int n1 = 1,n2 = 2; int temp = n2; while(n>2){ temp = n1+temp; n1 = n2; n2 = temp; n--; } return temp; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
文章来源: lion-wu.blog.csdn.net,作者:看,未来,版权归原作者所有,如需转载,请联系作者。
原文链接:lion-wu.blog.csdn.net/article/details/107593297
- 点赞
- 收藏
- 关注作者


评论(0)