【LeetCode】递归:原理入门+复杂度计算+练手试题
递归原理
每当递归函数调用自身时,它都会将给定的问题拆解为子问题。递归调用继续进行,直到到子问题无需进一步递归就可以解决的地步。
为了确保递归函数不会导致无限循环,它应具有以下属性:
一个简单的基本案例(basic case)(或一些案例) —— 能够不使用递归来产生答案的终止方案。 一组规则,也称作递推关系(recurrence relation),可将所有其他情况拆分到基本案例。
- 1
- 2
注意,函数可能会有多个位置进行自我调用。
先来个简单题目做做:
简单题:原地翻转字符串
编写一个函数,其作用是将输入的字符串反转过来。输入字符串以字符数组 char[] 的形式给出。
不要给另外的数组分配额外的空间,你必须原地修改输入数组、使用 O(1) 的额外空间解决这一问题。
你可以假设数组中的所有字符都是 ASCII 码表中的可打印字符。
示例 1:
输入:["h","e","l","l","o"]
输出:["o","l","l","e","h"]
示例 2:
输入:["H","a","n","n","a","h"]
输出:["h","a","n","n","a","H"]
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
思路
- 从输入字符串中获取前导字符和尾随字符,即 str[0] and str[n-1]
- 就地交换前导字符和末尾字符
- 递归调用函数来反转剩余的字符串,也就是 reverseString(str[1…n-2])
代码实现
void reverseChar(vector<char>& s,int begin,int end){ char temp = s[begin]; s[begin] = s[end]; s[end] = temp; } void reverseString(vector<char>& s) { int i = 0,j = s.size()-1; while(i<j){ reverseChar(s,i,j); i++; j--; } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
递归函数
对于一个问题,如果存在递归解决方案,我们可以按照以下步骤来实施它。
举个例子,我们将问题定义为有待实现的函数 F(X),其中 X 是函数的输入,同时也定义了问题的范围。
然后,在函数 F(X)中,我们将会:
将问题逐步分解成较小的范围,例如 x0∈X, x1∈X, ..., xn∈X; 调用函数 F(x0), F(x1), ..., F(xn) 递归地 解决 X 的这些子问题; 最后,处理调用递归函数得到的结果来解决对应 X 的问题。
- 1
- 2
- 3
再看一题:两两交换链表中的节点
给定一个链表,两两交换其中相邻的节点,并返回交换后的链表。
你不能只是单纯的改变节点内部的值,而是需要实际的进行节点交换。
示例:
给定 1->2->3->4, 你应该返回 2->1->4->3.
- 1
- 2
代码实现
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public: ListNode* swapPairs(ListNode* head) { if(head == NULL || head->next == NULL) return head; ListNode* temp = head->next; head->next = temp->next; temp->next = head; head->next = swapPairs(head->next); return temp; }
};
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
递推关系
在实现递归函数之前,有两件重要的事情需要解决:基本情况和递推关系。
递推关系: 一个问题的结果与其子问题的结果之间的关系。 基本情况: 不需要进一步的递归调用就可以直接计算答案的情况。 有时,基本案例也被称为 bottom cases,因为它们往往是问题被减
- 1
- 2
少到最小规模的情况,也就是如果我们认为将问题划分为子问题是一种自上而下的方式的最下层。
一旦我们计算出以上两个元素,再想要实现一个递归函数,就只需要根据递推关系调用函数本身,直到其抵达基本情况。
- 1
看个例子:
示例:杨辉三角

在杨辉三角中,每个数是它左上方和右上方的数的和。
给定一个非负整数 numRows,生成杨辉三角的前 numRows 行。
示例:
输入: 5
输出:
[ [1], [1,1], [1,2,1],
[1,3,3,1],
[1,4,6,4,1]
]
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
思路
递推关系
首先,我们定义一个函数 f(i,j),它将会返回杨辉三角第 i 行、第 j 列的数字。
我们可以用下面的公式来表示这一递推关系:
f(i,j)=f(i−1,j−1)+f(i−1,j)
- 1
基本情况
可以看到,每行的最左边和最右边的数字是基本情况,在这个问题中,它总是等于 1。
因此,我们可以将基本情况定义如下:
f(i,j)=1 where j=1 or j=i
- 1
正如我们所看到的,一旦我们定义了 递推关系 和 基本情况,递归函数的实现变得更加直观,特别是在我们用数学公式表示出这两个元素之后。
代码实现
vector<vector<int>> generate(int numRows) { vector<vector<int>> ret; if (numRows == 0) return ret; vector<int> t1 = { 1 }; ret.push_back(t1); if (numRows == 1) return ret; for (int j = 1; j < numRows; j++) { vector<int> temp(j, 0); temp[0] = 1; for (int i = 1; i < j; i++) { temp[i] = ret[j - 1][i - 1] + ret[j - 1][i]; } temp.push_back(1); ret.push_back(temp); } return ret; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
简单题:打印杨辉三角的第k行
你可以优化你的算法到 O(k) 空间复杂度吗?
代码实现
vector<int> getRow(int rowIndex) { vector<int> ret(rowIndex+1,0); ret[0] = 1; if (rowIndex == 0) return ret; for (int j = 1; j <= rowIndex; j++) { for (int i = j-1; i >0; i--) { ret[i] = ret[i - 1] + ret[i]; } ret[j] = 1; } return ret; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
记忆化:去除递归中的重复计算
通常情况下,递归是一种直观而有效的实现算法的方法。 但是,如果我们不明智地使用它,可能会给性能带来一些不希望的损失,例如重复计算。
为了演示重复计算的问题,让我们看一个大多数人可能都很熟悉的例子,斐波那契数。 如果我们定义函数 F(n) 表示在索引 n 处的斐波那契数,那么你可以推导出如下的递推关系:
F(n) = F(n - 1) + F(n - 2)
- 1
基本情况:
F(0) = 0, F(1) = 1
- 1
现在,如果你想知道 F(4) 是多少,你可以应用上面的公式并进行展开:
F(4) = F(3) + F(2) = (F(2) + F(1)) + F(2)
- 1
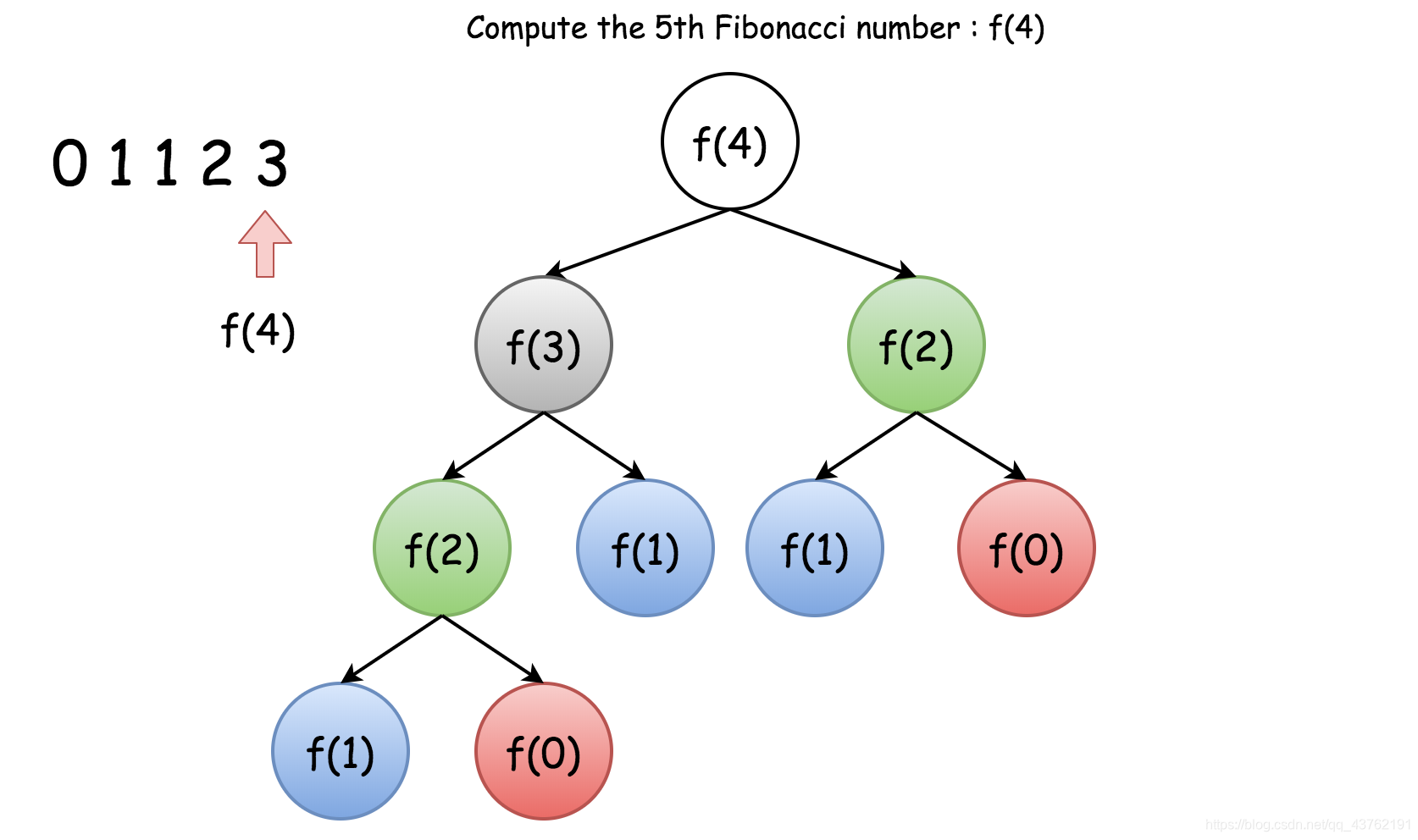
正如你所看到的,为了得到 f (4)的结果,我们需要在上述推导之后计算两次数 F(2) : 第一次在 F(4) 的第一次展开中,第二次在中间结果 F(3) 中。
下面的树显示了在计算 F(4) 时发生的所有重复计算(按颜色分组)。
记忆化
为了消除上述情况中的重复计算,正如许多人已经指出的那样,其中一个想法是将中间结果存储在缓存中,以便我们以后可以重用它们,而不需要重新计算。
这个想法也被称为记忆化,这是一种经常与递归一起使用的技术。
回到斐波那契函数 F(n)。 我们可以使用哈希表来跟踪每个以 n 为键的 F(n) 的结果。 散列表作为一个缓存,可以避免重复计算。 记忆化技术是一个很好的例子,它演示了如何通过增加额外的空间以减少计算时间。
题目:爬楼梯
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
注意:给定 n 是一个正整数。
示例 1:
输入: 2
输出: 2
解释: 有两种方法可以爬到楼顶。
1. 1 阶 + 1 阶
2. 2 阶
- 1
- 2
- 3
- 4
- 5
- 6
- 7
示例 2:
输入: 3
输出: 3
解释: 有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
思路(动态规划)
不难发现,这个问题可以被分解为一些包含最优子结构的子问题,即它的最优解可以从其子问题的最优解来有效地构建,我们可以使用动态规划来解决这一问题。
第 iii 阶可以由以下两种方法得到:
在第 (i−1) 阶后向上爬一阶。 在第 (i−2) 阶后向上爬 2 阶。
- 1
- 2
- 3
所以到达第 iii 阶的方法总数就是到第 (i−1) 阶和第 (i−2) 阶的方法数之和。
令 dp[i] 表示能到达第 iii 阶的方法总数:
dp[i]=dp[i−1]+dp[i−2]
- 1
代码实现
int climbStairs(int n) { if(n == 1) return 1; int n1 = 1,n2 = 2; int temp = n2; while(n>2){ temp = n1+temp; n1 = n2; n2 = temp; n--; } return temp; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
复杂度分析
给出一个递归算法,其时间复杂度 O(T) 通常是递归调用的数量(记作 R) 和计算的时间复杂度的乘积(表示为 O(s)的乘积:
O(T)=R∗O(s)
- 1
示例
在反转字符串问题中,我们需要以相反的顺序打印字符串,解决问题的递归关系可以表示如下:
printReverse(str) = printReverse(str[1…n]) + print(str[0])
其中 str[1…n] 是输入字符串 str 的子串,仅不含前导字符 str[0]。
如您所见,该函数将被递归调用 n 次,其中 n 是输入字符串的大小。在每次递归结束时,我们只是打印前导字符,因此该特定操作的时间复杂度是恒定的,即 O(1)。
总而言之,我们的递归函数 printReverse(str) 的总体时间复杂度为 O(printReverse)=n∗O(1)=O(n)
执行树
有时候,复杂度并不好算。
这时候,最好采用 执行树。
这是一个用于表示递归函数的执行流程的树。树中的每个节点都表示递归函数的调用。因此,树中的节点总数对应于执行期间的递归调用的数量。
递归函数的执行树将形成 n 叉树,其中 n 作为递推关系中出现递归的次数。例如,斐波那契函数的执行将形成二叉树,下面的图示展现了用于计算斐波纳契数 f(4) 的执行树。
示例

在 n 层的完全二叉树中,节点的总数为 2^n-1。因此 f(n) 中递归数目的上限(尽管不严格)也是 2^n−1。那么我们可以估计 f(n) 的时间复杂度为 O(2^n)。
记忆化
记忆化技术可以大大减少递归调用的数量,即减少执行树中的分支数量。在使用记忆化分析递归算法的时间复杂度时,也应该考虑到这种减少。
让我们回到斐波纳契数的例子。通过记忆化技术,我们保存每个索引 n 对应的的斐波那契数的结果。我们确信每个斐波那契数的计算只会发生一次。而从递推关系来看,斐波纳契数 f(n) 将取决于其所有 n-1 个先验斐波纳契数。结果,计算 f(n) 的递归将被调用 n-1 次以计算它所依赖的所有先验数字。
现在,我们可以简单地应用我们在上一部分介绍的公式来计算时间复杂度,即 O(1)∗n=O。记忆化技术不仅可以优化算法的时间复杂度,还可以简化时间复杂度的计算。
空间复杂度
在计算递归算法的空间复杂度时,应该考虑造成空间消耗的两个部分:递归相关空间(recursion related space)和非递归相关空间(non-recursion related space)。
递归相关空间是指由递归直接引起的内存开销,即用于跟踪递归函数调用的堆栈。为了完成典型的函数调用,系统应该在栈中分配一些空间来保存三个重要信息:
函数调用的返回地址。一旦函数调用完成,程序应该知道返回的位置,即函数调用之前的点; 传递给函数调用的参数; 函数调用中的局部变量。.
- 1
- 2
- 3
栈中的这个空间是函数调用期间产生的最小成本。然而,一旦完成函数调用,就会释放该空间。
对于递归算法,函数调用将连续链接直到它们到达基本情况(也称为 底层情况)。这意味着用于每个函数调用的空间也会累积。
对于递归算法,如果没有产生其他内存消耗,则此递归引起的空间将是算法的空间上限。
- 1
不管是否递归,你都可能需要在任何函数调用之前将问题的输入存储为全局变量。你可能还需要保存递归调用的中间结果。后者就是我们前面提到过的记忆化技术。因此,在分析空间复杂度时,我们应该考虑到因采用记忆化技术所导致的空间成本。
尾递归
尾递归函数是递归函数的一种,其中递归调用是递归函数中的最后一条指令。并且在函数中应该只有一次递归调用。
尾递归的好处是,它可以避免递归调用期间栈空间开销的累积,因为系统可以为每个递归调用重用栈中的固定空间。
示例
例如,对于递归调用序列 f(x1) -> f(x2) -> f(x3),如果函数 f(x) 以尾递归的形式实现。那么其执行步骤的顺序和栈空间的分配如下所示:
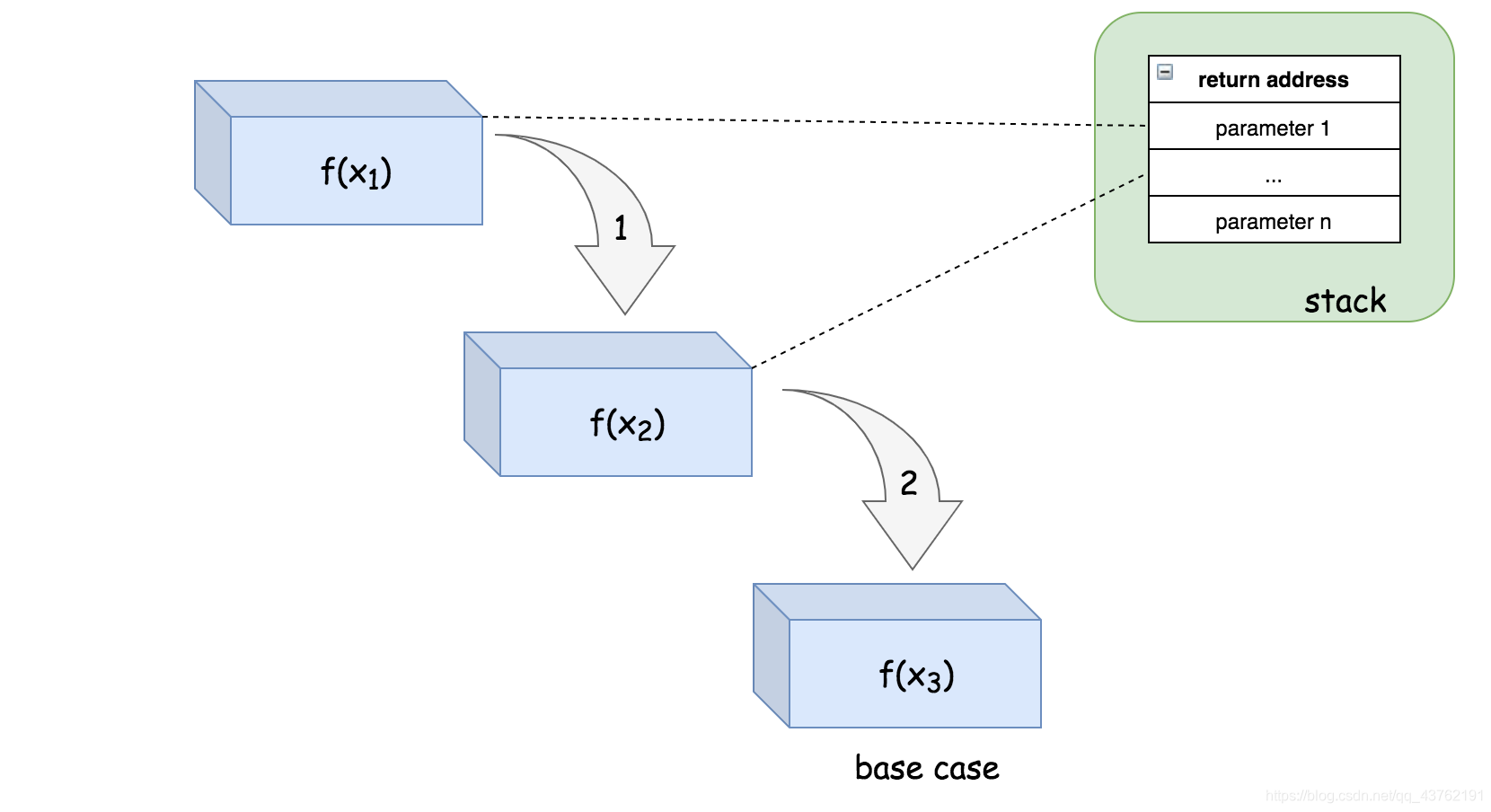
请注意,在尾递归的情况下,一旦从递归调用返回,我们也会立即返回,因此我们可以跳过整个递归调用返回链,直接返回到原始调用方。这意味着我们根本不需要所有递归调用的调用栈,这为我们节省了空间。
例如,在步骤(1)中,栈中的一个空间将被分配给 f(x1),以便调用 f(x2)。然后,在步骤(2)中,函数 f(x2) 能够递归地调用 f(x3),但是,系统不需要在栈上分配新的空间,而是可以简单地重用先前分配给第二次递归调用的空间。最后,在函数 f(x3) 中,我们达到了基本情况,该函数可以简单地将结果返回给原始调用方,而不会返回到之前的函数调用中。
尾递归函数可以作为非尾递归函数来执行,也就是说,带有调用栈并不会对结果造成影响。通常,编译器会识别尾递归模式,并优化其执行。然而,并不是所有的编程语言都支持这种优化,比如 C,C++ 支持尾递归函数的优化。另一方面,Java 和 Python 不支持尾递归优化。
题目:二叉树的最大深度
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
代码实现
int maxDepth(TreeNode* root) { if(root == NULL) return 0; return 1 + max(maxDepth(root->left), maxDepth(root->right)); }
- 1
- 2
- 3
- 4
- 5
总结
作为提醒,下面是解决递归问题的一般工作流程:
定义递归函数; 写下递归关系和基本情况; 使用memoization(记忆化)以消除重复计算问题(如果存在)。 尽可能地实现 尾递归(tail recursion)函数,以优化空间复杂度。
- 1
- 2
- 3
- 4
当有疑问时,写下重复出现的关系。
只要有可能,就应用记忆化。
当堆栈溢出时,尾递归可能会有所帮助。
习题:合并两个有序链表
ListNode mergeTwoLists(ListNode l1, ListNode l2) { if (l1 == NULL) { return l2; } else if (l2 == NULL) { return l1; } else if (l1.val < l2.val) { l1.next = mergeTwoLists(l1.next, l2); return l1; } else { l2.next = mergeTwoLists(l1, l2.next); return l2; } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
作者:力扣 (LeetCode)
链接:https://leetcode-cn.com/leetbook/read/recursion/4x8bc/
来源:力扣(LeetCode) 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
文章来源: lion-wu.blog.csdn.net,作者:看,未来,版权归原作者所有,如需转载,请联系作者。
原文链接:lion-wu.blog.csdn.net/article/details/107778526
- 点赞
- 收藏
- 关注作者


评论(0)