【回溯算法】N叉树相关技巧

我个人认为，想玩得转回溯算法，N叉树的遍历是必备的。于是我就来把这块石头搬开。

前言

二叉树是一棵以根节点开始，每个节点含有不超过 2 个子节点的树。让我们将这个定义扩展到 N 叉树 。 一棵以根节点开始，每个节点不超过 N 个子节点的树，称为 N叉树 。
各位自行脑补。

N叉树的遍历

回顾 - 二叉树的遍历

前序遍历 - 首先访问根节点，然后遍历左子树，最后遍历右子树；
中序遍历 - 首先遍历左子树，然后访问根节点，最后遍历右子树；
后序遍历 - 首先遍历左子树，然后遍历右子树，最后访问根节点；
层序遍历 - 按照从左到右的顺序，逐层遍历各个节点。

   

  

   
1
   
2
   
3
   
4
  

N 叉树的中序遍历没有标准定义，中序遍历只有在二叉树中有明确的定义。
我们跳过 N 叉树中序遍历的部分。

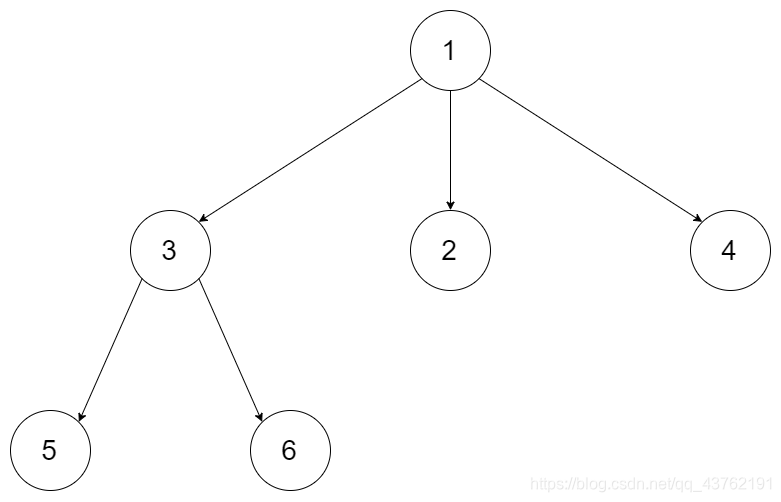
后面的栗子都用这个图了

数据结构

class Node {
public: int val; vector<Node*> children; Node() {} Node(int _val) { val = _val; } Node(int _val, vector<Node*> _children) { val = _val; children = _children; }
};

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
 

N叉树的前序遍历

给定一个 N 叉树，返回其节点值的前序遍历。

代码实现

class Solution {
public: void preorderDFS(Node* root, int index, vector<int>& ret) { if (root == NULL) return; ret.push_back(root->val); int sz = (root->children).size(); while (index < sz) { preorderDFS(root->children[index], 0, ret); index += 1; } } vector<int> preorder(Node* root) { vector<int> ret; preorderDFS(root, 0, ret); return ret; }
};

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
 

后序遍历

给定一个 N 叉树，返回其节点值的后序遍历。

代码实现

class Solution {
public: void postorderDFS(Node* root, int index, vector<int>& ret) { if (root == NULL) return; int sz = (root->children).size(); while (index < sz) { postorderDFS(root->children[index], 0, ret); index += 1; } ret.push_back(root->val); } vector<int> postorder(Node* root) { vector<int> ret; postorderDFS(root, 0, ret); return ret; }
};

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
 

层序遍历

给定一个 N 叉树，返回其节点值的层序遍历。 (即从左到右，逐层遍历)。

class Solution {
public: vector<vector<int>> result; void dfs(Node* root, int dep){ if(!root) return; if(dep == result.size()) result.emplace_back(); result[dep].push_back(root->val); auto children = root->children; for(auto ele:children){ dfs(ele, dep+1); } } vector<vector<int>> levelOrder(Node* root) { dfs(root, 0); return result; }
};

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
 

N叉树的经典递归解法

1. "自顶向下"的解决方案

   "自顶向下"意味着在每个递归层次上，我们首先访问节点以获得一些值，然后在调用递归函数时，将这些值传给其子节点。

一个典型的 “自顶向下” 函数 top_down(root, params) 的工作原理如下：

1. 对于 null 节点返回一个特定值
2. 如果有需要，对当前答案 answer 进行更新 // answer <-- params
3. for each child node root.children[k]:

4.  ans[k] = top_down(root.children[k], new_params[k])  // new_params <-- root.val, params
   
        
   
       
   
        
   1
       

5. 如果有需要，返回答案 answer // answer <-- all ans[k]

1. "自底向上"的解决方案

   “自底向上” 意味着在每个递归层次上，我们首先为每个子节点递归地调用函数，然后根据返回值和根节点本身的值给出相应结果。

一个典型的 “自底向上” 函数 bottom_up(root) 的工作原理如下：

1.对于 null 节点返回一个特定值
2.for each child node root.children[k]:
3. ans[k] = bottom_up(root.children[k]) // 为每个子节点递归地调用函数
4. 返回答案 answer // answer <- root.val, all ans[k]

作者：力扣 (LeetCode)
链接：https://leetcode-cn.com/leetbook/read/n-ary-tree/x0ucsg/
来源：力扣（LeetCode） 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

N叉树的最大深度

给定一个 N 叉树，找到其最大深度。
最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。

class Solution {
public: int maxDepth(Node* root) {
		if (root == NULL)return 0;
		int height = 0;
		for (int i = 0; i < root->children.size(); i++) { height = max(height, maxDepth(root->children[i]));
		}
		return height + 1;
	}
};

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
 

文章来源: lion-wu.blog.csdn.net，作者：看，未来，版权归原作者所有，如需转载，请联系作者。

原文链接：lion-wu.blog.csdn.net/article/details/107857837