深度学习的几个重要的词语概念

batch

深度学习的优化算法，即梯度下降。有批梯度下降，随机梯度下降

第一种，遍历全部数据集算一次损失函数，然后算函数对各个参数的梯度，更新梯度。使用batch梯度下降法时，每次迭代你都需要历遍整个训练集，这称为Batch gradient descent，批梯度下降。这个算法每个迭代需要处理大量训练样本，该算法的主要弊端在于特别是在训练样本数量巨大的时候，单次迭代耗时太长。如果训练样本不大，batch梯度下降法运行地很好。

另一种，每输入一个数据就算一下损失函数，然后求梯度更新参数，这个称为随机梯度下降，stochastic gradient descent。使用随机梯度下降法，如果你只要处理一个样本，那这个方法很好，这样做没有问题，通过减小学习率，噪声会被改善或有所减小。
但随机梯度下降法的一大缺点是，你会失去所有向量化带给你的加速，因为一次性只处理了一个训练样本，这样效率过于低下。并且收敛性能不太好，可能在最优点附近晃来晃去，hit不到最优点
这种可以理解为mini-batch的一个极端情况，假设mini-batch大小为1，就有了新的算法，叫做随机梯度下降法，每个样本都是独立的mini-batch。

为了中和两种方法的缺点，现在一般采用的是一种折中手段，mini-batch gradient decent，小批的梯度下降，这种方法把数据分为若干个批，把训练集分割为小一点的子集训练，这些子集被取名为mini-batch，按子集来更新参数，这样，一个子集中的一组数据共同决定了本次梯度的方向，下降起来就不容易跑偏，减少了随机性。另一方面因为批的样本数与整个数据集相比小了很多，计算量也不是很大。

iterations

iterations（迭代）：每一次迭代都是一次权重更新，每一次权重更新需要batch_size个数据进行Forward运算得到损失函数，再BP算法更新参数。1个iteration等于使用batchsize个样本训练一次。

epochs

epochs被定义为向前和向后传播中所有批次的单次训练迭代。这意味着1个周期是整个输入数据集的一次向前和向后传递。简单说，一次epochs指的就是全部的数据集跑了一轮（遍）。
训练集有100个样本，batchsize=10，那么：
训练完整个样本集需要：
10次iteration，1次epoch。

具体的计算公式为：
one epoch = numbers of iterations = N = 训练样本的数量/batch_size

Vanishing / Exploding gradients

梯度消失/梯度爆炸
训练神经网络，尤其是深度神经所面临的一个问题就是梯度消失或梯度爆炸，也就是你训练神经网络的时候，导数或坡度有时会变得非常大，或者非常小，甚至于以指数方式变小，这加大了训练的难度。

正则化（Regularization）

深度学习可能存在过拟合问题——高方差，有两个解决方法，一个是正则化，另一个是准备更多的数据，这是非常可靠的方法，但你可能无法时时刻刻准备足够多的训练数据或者获取更多数据的成本很高，但正则化通常有助于避免过拟合或减少你的网络误差。

underfitting/overfitting（欠拟合和过拟合）

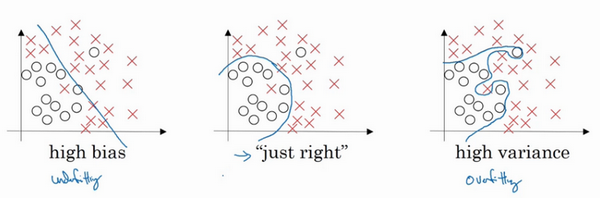
假设这就是数据集，如果给这个数据集拟合一条直线，可能得到一个逻辑回归拟合，但它并不能很好地拟合该数据，这是高偏差（high bias）的情况，我们称为“欠拟合”（underfitting）。

相反的如果我们拟合一个非常复杂的分类器，比如深度神经网络或含有隐藏单元的神经网络，可能就非常适用于这个数据集，但是这看起来也不是一种很好的拟合方式分类器方差较高（high variance），数据过度拟合（overfitting）。

在两者之间，可能还有一些像图中这样的，复杂程度适中，数据拟合适度的分类器，这个数据拟合看起来更加合理，我们称之为“适度拟合”（just right）是介于过度拟合和欠拟合中间的一类。

channels（通道）/feature map/卷积核数量

在CNN中初始的通道是输入的图像的通道的大小，彩色的RGB的通道是3个，黑白图像只有一层通道，之后每一层输出的通道数，是每一层的卷积核的个数（每一个卷积核代表提取一种特征）
上面的说法是tensorflow等框架中的参数中的表示，另一种说法：

• 在输入层，如果是灰度图片，那就只有一个feature map；如果是彩色图片，一般就是3个feature map（红绿蓝）。
• 层与层之间会有若干个卷积核（kernel）（也称为过滤器），上一层每个feature map跟每个卷积核做卷积，都会产生下一层的一个feature map，有N个卷积核，下层就会产生N个feature map。而每一个卷积核的通道数（feature map）就是上层的通道数（feature map）大小（因为要对应起来进行想乘求和）

kernel卷积核/filter过滤器

如上图，3×3×3的就是卷积核或者叫做特征过滤器，卷积核进行对3维卷积操作之后得到4×4输出特征。

为了计算这个卷积操作的输出，你要做的就是把这个3×3×3的过滤器先放到最左上角的位置，这个3×3×3的过滤器有27个数，27个参数就是3的立方。依次取这27个数，然后乘以相应的红绿蓝通道中的数字。先取红色通道的前9个数字，然后是绿色通道，然后再是蓝色通道，乘以左边黄色立方体覆盖的对应的27个数，然后把这些数都加起来，就得到了输出的第一个数字。

  

 

  
1
 

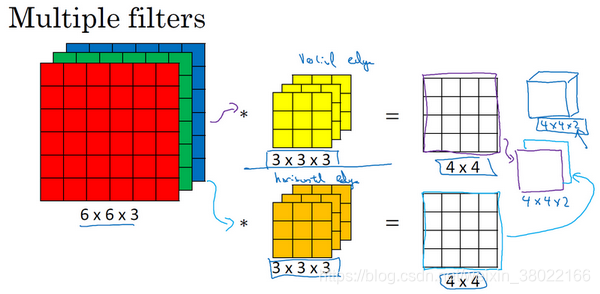
双特征（第一个）这可能是一个垂直边界检测器或者是学习检测其他的特征。第二个过滤器可以用橘色来表示，它可以是一个水平边缘检测器。
所以和第一个过滤器卷积，可以得到第一个4×4的输出，然后卷积第二个过滤器，得到一个不同的4×4的输出。我们做完卷积，然后把这两个4×4的输出，取第一个把它放到前面，然后取第二个过滤器输出。所以把这两个输出堆叠在一起，这样你就都得到了一个4×4×2的输出立方体。

你可以把这个立方体当成一个的盒子，所以这就是一个4×4×2的输出立方体。它用6×6×3的图像，然后卷积上这两个不同的3×3的过滤器，得到两个4×4的输出，它们堆叠在一起，形成一个4×4×2的立方体，这里的2的来源于我们用了两个不同的过滤器。

  

 

  
1
 

而这个2就是新的通道channels个数
每个卷积核具有长宽深三个维度；一个filter等同于一个卷积核：只是指定了卷积核的长宽深
在某个卷积层中，可以有多个卷积核：下一层需要多少个channels（feature map），本层就需要多少个卷积核。

• 最初输入的图片样本的 channels ，取决于图片类型，比如RGB；
• 卷积核中的 in_channels ，就是要操作的图像数据的feature map张数，也就是卷积核的深度。
• 卷积操作完成后输出的 out_channels ，取决于卷积核的数量（下层将产生的feature map数量）。此时的 out_channels 也会作为下一次卷积时的卷积核的 in_channels。

参考:
CNN中feature map、卷积核、卷积核个数、filter、channel的概念解释，以及CNN 学习过程中卷积核更新的理解

文章来源: blog.csdn.net，作者：αβγθ，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/weixin_38022166/article/details/106853557