邻接矩超详解(C/C++)
提示:记得点赞,关注,收藏
前言
图的结构比较复杂,任何两个顶点之间都可能有关系。如果采用顺序存储,则需要使用二维数组表示元素之间的关系,即邻接矩阵(Adjacency Matrix),也可以使用边集数组,把,每条边顺序存储起来。如果采用链式存储,则有邻接表.十字链表和邻接多重表等表示方法。其中,邻接矩阵和邻接表是最简单、最常用的存储方法。。
提示:以下是本篇文章正文内容,本篇文章参考《算法训练营》
一、领接矩阵
1.概念
邻接矩阵通常采用一个一维数组存储图中节点的信息,采用一个二维数组存储图中节点之间的邻接关系。
2.分类
1. 邻接矩阵的表示方法
无向图、有向图和网的邻接矩阵的表示方法如下所述。
(1)无向图的邻接矩阵
在无向图中,若从节点vi 到节点vj 有边,则邻接矩阵 M [i ][j ]= M [j ][i ]=1,否则 M [i ][j ]=0。
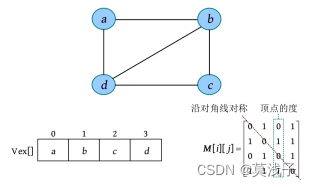
例如,一个无向图的节点信息和邻接矩阵如下图所示。在该无向图中,从节点a 到节点b 有边,从节点b 到节点a 也有边,节点a 、b 在一维数组中的存储位置分别为0、1,则 M [0][1]= M [1][0]=1。
无向图的邻接矩阵的特点如下。
(1)无向图的邻接矩阵是对称矩阵,并且是唯一的。
(2)第i 行或第i 列非零元素的个数正好是第i 个节点的度。上图中的邻接矩阵,第3列非零元素的个数为2,说明第3个节点c 的度为2。
(2)有向图的邻接矩阵
在有向图中,若从节点vi 到节点vj 有边,则邻接矩阵 M [i ][j ]=1,否则 M [i ][j ]=0。
注意: 以尖括号<vi ,vj >表示的是有序对,以圆括号(vi ,vj )表示的是无序对,后同。
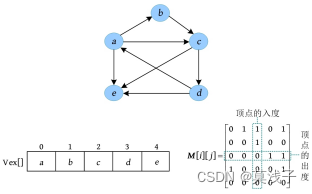
例如,一个有向图的节点信息和邻接矩阵如下图所示。在该有向图中,从节点a 到节点b 有边,节点a 、b 在一维数组中的存储位置分别为0、1,因此 M [0][1]=1。有向图中的边是有向边,从节点a 到节点b 有边,从节点b 到节点a 不一定有边,因此有向图的邻接矩阵不一定是对称的。
有向图的邻接矩阵的特点如下
(1)有向图的邻接矩阵不一定是对称的。
(2)第i 行非零元素的个数正好是第i 个节点的出度,第i 列非零元素的个数正好是第i 个节点的入度。上图中的邻接矩阵,第3行非零元素的个数为2,第3列非零元素的个数也为2,说明第3个节点c 的出度和入度均为2。
3)网的邻接矩阵
网是带权图,需要存储边的权值,则邻接矩阵表示为其中,wij 表示边上的权值,∞表示无穷大。当i =j 时,wii 也可被设置为0。
例如,一个网的节点信息和邻接矩阵如下图所示。在该网中,从节点a 到节点b 有边,且该边的权值为2,节点a 、b 在一维数组中的存储位置分别为0、1,因此 M [0][1]=2。从节点b 到节点a 没有边,因此 M [1][0]=∞。
3.步骤
算法步骤:
(1)输入节点数和边数;
(2)依次输入节点信息,将其存储到节点数组Vex[]中;
(3)初始化邻接矩阵,如果是图,则将其初始化为0;如果是网,则将其初始化为∞;
(4)依次输入每条边依附的两个节点,如果是网,则还需要输入该边的权值。
• 如果是无向图,则输入a b ,查询节点a、b 在节点数组Vex[]中的存储下标i 、j ,令Edge[i ][j ]=Edge[j ][i ]=1。
• 如果是有向图,则输入a b ,查询节点a、b 在节点数组Vex[]中的存储下标i 、j ,令Edge[i ][j ]=1。
• 如果是无向网,则输入a b w ,查询节点a、b 在节点数组Vex[]中的存储下标i 、j ,令Edge[i ][j ]=Edge[j ][i ]=w 。
• 如果是有向网,则输入a b w ,查询节点a、b 在节点数组Vex[]中的存储下标i 、j ,令Edge[i ][j ]=w 。
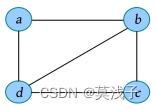
完美图解: 一个无向图如下图所示,其邻接矩阵的存储过程如下所述。
(1)输入节点数和边数。
4 5
结果:G .vexnum=4、G .edgenum=5。
(2)输入节点信息,将其存入节点信息数组。
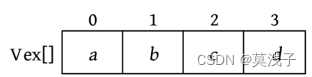
a b c d
(3)初始化邻接矩阵的值均为0,如下图所示。
(4)依次输入每条边依附的两个节点。
• 输入a b ,处理结果:在Vex[]数组中查找到节点a 、b 的下标分别为0、1,是无向图,因此令 Edge[0][1]=Edge[1][0]=1,如下图所示。
• 输入a d ,处理结果:在Vex[]数组中查找到节点a 、d 的下标分别为0、3,是无向图,因此令Edge[0][3]= Edge[3][0]=1,如下图所示。
• 输入b c ,处理结果:在Vex[]数组中查找到节点b 、c 的下标分别为1、2,是无向图,因此令Edge[1][2]= Edge[2][1]=1,如下图所示。
• 输入b d ,处理结果:在Vex[]数组中查找到节点b 、d 的下标分别为1、3,是无向图,因此令Edge[1][3]= Edge[3][1]=1,如下图所示。
• 输入c d ,处理结果:在Vex[]数组中查找到节点c 、d 的下标分别为2、3,是无向图,因此令Edge[2][3]= Edge[3][2]=1,如下图所示。
在实际应用中,也可以先输入节点信息并将其存入数组Vex[]。在输入边时直接输入节点的存储下标序号,这样可以节省查询节点下标所需的时间,从而提高效率。
4. 邻接矩阵的优缺点
(1)优点如下。
• 快速判断在两节点之间是否有边。在图中,Edge[i ][j ]=1,表示有边;Edge[i ][j ]=0,表示无边。在网中,Edge[i ][j ]=∞,表示无边,否则表示有边。时间复杂度为O (1)。
• 方便计算各节点的度。在无向图中,邻接矩阵第i 行元素之和就是节点i 的度;在有向图中,第i 行元素之和就是节点i 的出度,第i 列元素之和就是节点i 的入度。时间复杂度为O (n )。
(2)缺点如下。
• 不便于增删节点。增删节点时,需要改变邻接矩阵的大小,效率较低。
• 不便于访问所有邻接点。访问第i 个节点的所有邻接点时,需要访问第i 行的所有元素,时间复杂度为O (n )。访问所有节点的邻接点,时间复杂度为O (n 2 )。
• 空间复杂度高,为O (n 2 )。
在实际应用中,如果在一个程序中只用到一个图,就可以用一个二维数组表示邻接矩阵,直接输入节点的下标,省去节点信息查询步骤。有时如果图无变化,则为了方便,可以省去输入操作,直接在程序头部定义邻接矩阵。
5.代码
领接矩阵存储结构创建
无向图代码如下
- 点赞
- 收藏
- 关注作者



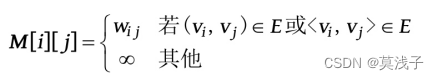


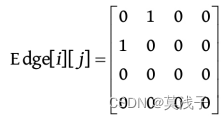

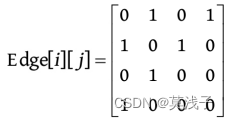
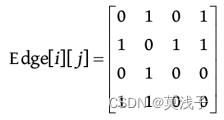

评论(0)