基于遗传模拟退火混合优化算法的车间作业最优调度matlab仿真,输出甘特图

1.程序功能描述
        车间作业调度问题（Job Shop Scheduling Problem, JSSP）是一种典型的生产调度问题，旨在确定一系列作业在多个并行工作中心上的加工顺序和起止时间，以最小化总完成时间、最大完工时间、机器闲置时间等目标。

2.测试软件版本以及运行结果展示
MATLAB2022a版本运行

3.核心程序

       % 交叉操作
       Pop0{j2}=func_cross(Bestp{j2},Pop0{j2},l2,l1);
       Pop0{j2}=func_cross(bestparticle1,Pop0{j2},l4,l3); 
   end 
   Fitjob=[Fitjob,minval];
 
 
   if jj == 1
      [x1,x2,x3]=func_decode2(bestparticle,Mjob,Mt,Nmach);
      disp('迭代1次时，最小流动时间，最大完工时间，最小间隙时间')
      [x1,x2,x3]
      figure
      func_gant(bestparticle,Pop0Long,Mjob,Mt,x2);
      title('迭代1次时甘特图');
   end
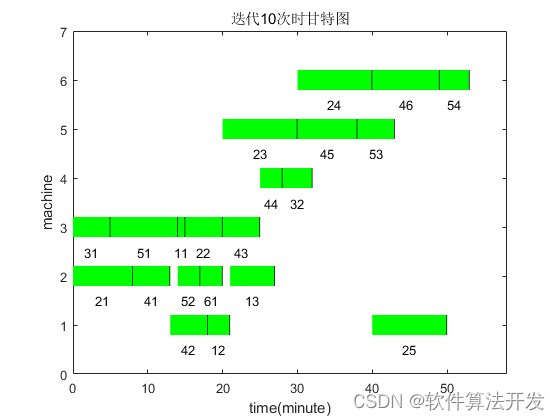
   if jj == 10
      [x1,x2,x3]=func_decode2(bestparticle,Mjob,Mt,Nmach);
      disp('迭代10次时，最小流动时间，最大完工时间，最小间隙时间')
      [x1,x2,x3]
      figure
      func_gant(bestparticle,Pop0Long,Mjob,Mt,x2);
      title('迭代10次时甘特图');
   end
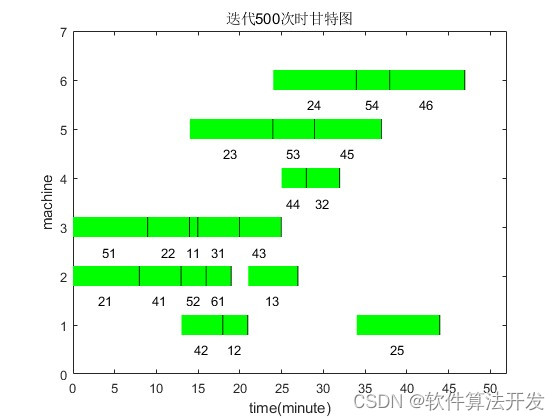
   if jj == 500
      [x1,x2,x3]=func_decode2(bestparticle,Mjob,Mt,Nmach);
      disp('迭代500次时，最小流动时间，最大完工时间，最小间隙时间')
      [x1,x2,x3]
      figure
      func_gant(bestparticle,Pop0Long,Mjob,Mt,x2);
      title('迭代500次时甘特图');
   end
end
 
 
figure;
plot(Fitjob);
xlabel('迭代次数');
ylabel('适应度收敛曲线');
39

4.本算法原理
4.1遗传算法与模拟退火算法简介
        遗传算法（Genetic Algorithm, GA）是一种基于自然选择和遗传机制的全局搜索算法。其主要组成部分包括：

编码（Encoding）：将作业调度问题转化为基因型表示，如作业列表、工序顺序、工作中心分配等信息。

种群初始化（Population Initialization）：创建一个包含多个个体（作业调度方案）的初始种群。

适应度评估（Fitness Evaluation）：根据优化目标（如总完成时间）计算每个个体的适应度值。

遗传操作（Genetic Operators）：包括选择、交叉（Crossover）、变异（Mutation），用于生成下一代种群。

终止条件（Termination Criteria）：设定最大迭代次数、收敛阈值等，决定算法何时停止。

       模拟退火算法（Simulated Annealing, SA）模拟固体材料在冷却过程中的退火现象，实现概率性接受非改进解以跳出局部最优。其主要步骤包括：

状态转移（State Transition）：基于当前解生成一个邻域解。

接受概率（Acceptance Probability）：

温度更新（Temperature Update）：随着迭代过程，逐步降低温度T，遵循降温策略如指数降温：

Tt+1​=αTt​

其中，α是冷却系数，通常取值在(0 < α<1)之间。

4.2 GSAHO算法应用于JSSP
编码：采用作业列表表示法（Job-List Representation），每个个体由n个子串组成，每个子串代表一个作业，子串内部按照工序顺序排列。例如，I = [i_1, i_2, ..., i_n]，其中i_j = [o_{j1}, o_{j2}, ..., o_{jm_j}]，o_{jk}表示作业j的第k道工序在工作中心上的起始时间。

适应度函数：根据优化目标定义适应度函数。以最小化最大完工时间（Makespan）为例，适应度函数为：

其中，C_{max}为最大完工时间，p_{jk}为作业j的第k道工序的加工时间，t_{jk}为其等待时间（由调度决定）。

遗传操作：采用轮盘赌选择、部分匹配交叉（PMX）和单点变异等遗传算子。

模拟退火：在遗传算法的基础上，引入模拟退火过程，每次迭代后以一定的接受概率接受非改进解，以增加种群的多样性并避免早熟收敛。