动手学深度学习需要这些数学基础知识

本附录总结了本书中涉及的有关线性代数、微分和概率的基础知识。为避免赘述本书未涉及的数学背景知识，本节中的少数定义稍有简化。

A.1　线性代数

下面分别概括了向量、矩阵、运算、范数、特征向量和特征值的概念。

A.1.1　向量

本书中的向量指的是列向量。一个n维向量x的表达式可写成

其中是向量的元素。我们将各元素均为实数的 n 维向量 x 记作或。

A.1.2　矩阵

一个m行n列矩阵的表达式可写成

其中是矩阵 X 中第 i 行第j列的元素（）。我们将各元素均为实数的 m 行 n列矩阵 X 记作。不难发现，向量是特殊的矩阵。

A.1.3　运算

设n维向量a中的元素为，n维向量b中的元素为。向量a与b的点乘（内积）是一个标量：

设两个m行n列矩阵

矩阵A的转置是一个n行m列矩阵，它的每一行其实是原矩阵的每一列：

两个相同形状的矩阵的加法是将两个矩阵按元素做加法：

我们使用符号表示两个矩阵按元素乘法的运算，即阿达马积（Hadamard product）：

定义一个标量k。标量与矩阵的乘法也是按元素做乘法的运算：

其他诸如标量与矩阵按元素相加、相除等运算与上式中的相乘运算类似。矩阵按元素开根号、取对数等运算也就是对矩阵每个元素开根号、取对数等，并得到和原矩阵形状相同的矩阵。

矩阵乘法和按元素的乘法不同。设A为m行p列的矩阵，B为p行n列的矩阵。两个矩阵相乘的结果

是一个m行n列的矩阵，其中第i 行第j 列（）的元素为

A.1.4　范数

设n维向量x中的元素为。向量x的范数为


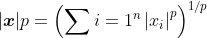
例如，x的范数是该向量元素绝对值之和：

而x的范数是该向量元素平方和的平方根：

我们通常用 || x || 指代 || x ||2。

设X是一个m行n列矩阵。矩阵X的Frobenius范数为该矩阵元素平方和的平方根：

其中为矩阵 X 在第 i 行第 j 列的元素。

A.1.5　特征向量和特征值

对于一个n 行n 列的矩阵A，假设有标量 λ 和非零的n维向量v使

那么 v 是矩阵 A 的一个特征向量，标量 λ 是 v 对应的特征值。

A.2　微分

我们在这里简要介绍微分的一些基本概念和演算。

B.2.1　导数和微分

假设函数的输入和输出都是标量。函数 f 的导数


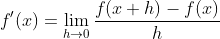
且假定该极限存在。给定 ，其中x和y分别是函数 f 的自变量和因变量。以下有关导数和微分的表达式等价：


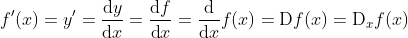
其中符号D和d/dx也叫微分运算符。常见的微分演算有DC = 0（C为常数）、（n为常数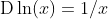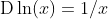）、、 等。

如果函数 f 和g都可导，设C为常数，那么

![\begin{aligned}\frac{\text{d}}{\text{d}x} [Cf(x)] &= C \frac{\text{d}}{\text{d}x} f(x)\\frac{\text{d}}{\text{d}x} [f(x) + g(x)] &= \frac{\text{d}}{\text{d}x} f(x) + \frac{\text{d}}{\text{d}x} g(x)\ \frac{\text{d}}{\text{d}x} [f(x)g(x)] &= f(x) \frac{\text{d}}{\text{d}x} [g(x)] + g(x) \frac{\text{d}}{\text{d}x} [f(x)]\\frac{\text{d}}{\text{d}x} \left[\frac{f(x)}{g(x)}\right] &= \frac{g(x) \frac{\text{d}}{\text{d}x} [f(x)] - f(x) \frac{\text{d}}{\text{d}x} [g(x)]}{[g(x)]^2}\end{aligned}](http://private.codecogs.com/gif.latex?\begin{aligned}&\frac{\text{d}}{\text{d}x}%20[Cf(x%29]%20=%20C%20\frac{\text{d}}{\text{d}x}%20f(x%29\&\frac{\text{d}}{\text{d}x}%20[f(x%29%20+%20g(x%29]%20=%20\frac{\text{d}}{\text{d}x}%20f(x%29%20+%20\frac{\text{d}}{\text{d}x}%20g(x%29\%20&\frac{\text{d}}{\text{d}x}%20[f(x%29g(x%29]%20=%20f(x%29%20\frac{\text{d}}{\text{d}x}%20[g(x%29]%20+%20g(x%29%20\frac{\text{d}}{\text{d}x}%20[f(x%29]\&\frac{\text{d}}{\text{d}x}%20\left[\frac{f(x%29}{g(x%29}\right]%20=%20\frac{g(x%29%20\frac{\text{d}}{\text{d}x}%20[f(x%29]%20-%20f(x%29%20\frac{\text{d}}{\text{d}x}%20[g(x%29]}{[g(x%29]^2}\end{aligned})

如果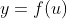和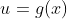都是可导函数，依据链式法则，

A.2.2　泰勒展开

函数 f 的泰勒展开式是


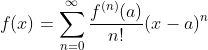
其中 为函数 f 的 n 阶导数（求n次导数），n! 为 n 的阶乘。假设是一个足够小的数，如果将上式中 x 和 a 分别替换成和 x，可以得到


由于足够小，上式也可以简化成


A.2.3　偏导数

设u为一个有n个自变量的函数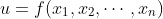，，它有关第i个变量的偏导数为


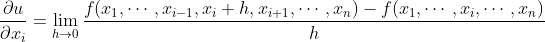
以下有关偏导数的表达式等价：

为了计算，只需将视为常数并求u有关xi的导数。

A.2.4　梯度

假设函数的输入是一个n维向量，输出是标量。函数有关 x 的梯度是一个由n个偏导数组成的向量：

![\nabla_{\boldsymbol{x}} f(\boldsymbol{x}) = \bigg[\frac{\partial f(\boldsymbol{x})}{\partial x_1}, \frac{\partial f(\boldsymbol{x})}{\partial x_2}, \ldots, \frac{\partial f(\boldsymbol{x})}{\partial x_n}\bigg]^\top](http://private.codecogs.com/gif.latex?\nabla_{\boldsymbol{x}}%20f(\boldsymbol{x}%29%20=%20\bigg[\frac{\partial%20f(\boldsymbol{x}%29}{\partial%20x_1},%20\frac{\partial%20f(\boldsymbol{x}%29}{\partial%20x_2},%20\cdots,%20\frac{\partial%20f(\boldsymbol{x}%29}{\partial%20x_n}\bigg]^\top)

为表示简洁，我们有时用  代替 。

假设x是一个向量，常见的梯度演算包括


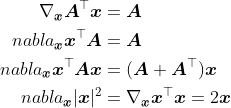
类似地，假设X是一个矩阵，那么

A.2.5　海森矩阵

假设函数的输入是一个n维向量，输出是标量。假定函数 f所有的二阶偏导数都存在，f 的海森矩阵H是一个n行n列的矩阵：

其中二阶偏导数为


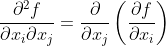
A.3　概率

最后，我们简要介绍条件概率、期望和均匀分布。

A.3.1　条件概率

假设事件A和事件B的概率分别为和，两个事件同时发生的概率记作 或。给定事件B，事件A的条件概率为


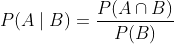
也就是说，


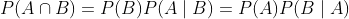
当满足


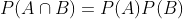
时，事件 A 和事件 B 相互独立。

A.3.2　期望

离散的随机变量X的期望（或平均值）为


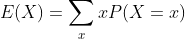
A.3.3　均匀分布

假设随机变量X服从[a, b]上的均匀分布，即。随机变量X取a和b之间任意一个数的概率相等。

小结

• 本附录总结了本书中涉及的有关线性代数、微分和概率的基础知识。

练习

求函数 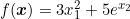 的梯度。

本文摘自《动手学深度学习》

动手学深度学习

作者：阿斯顿·张（Aston Zhang）, 李沐（Mu Li）, [美] 扎卡里·C. 立顿（Zachary C. Lipton）, [德] 亚历山大·J. 斯莫拉（Alexander J. Smola）

• 人工智能机器学习深度学习领域重磅教程图书

• 亚马逊科学家作品

• 动手学深度学习的全新模式，原理与实战紧密结合

目前市面上有关深度学习介绍的书籍大多可分两类，一类侧重方法介绍，另一类侧重实践和深度学习工具的介绍。本书同时覆盖方法和实践。本书不仅从数学的角度阐述深度学习的技术与应用，还包含可运行的代码，为读者展示如何在实际中解决问题。为了给读者提供一种交互式的学习体验，本书不但提供免费的教学视频和讨论区，而且提供可运行的Jupyter记事本文件，充分利用Jupyter记事本能将文字、代码、公式和图像统一起来的优势。这样不仅直接将数学公式对应成实际代码，而且可以修改代码、观察结果并及时获取经验，从而带给读者全新的、交互式的深度学习的学习体验。

本文转载自异步社区。

原文链接：https://www.epubit.com/articleDetails?id=NNb41d8566-df0d-4092-9d6b-8c43fb49fee1