2025-10-04：带权树中的最短路径。用go语言，给出一个节点编号为 1…n 的无向加权树，并以节点 1 作为根。用长度为 n−1 的数组 edges 描述每条边，edges[i] = [ui, vi, wi] 表示节点 ui 与 vi 之间存在一条权值为 wi 的无向边。

还给出一个长度为 q 的操作序列 queries，其中每个操作是两种类型之一：

• [1, u, v, w’]：把连接 u 与 v 的那条边的权重改为 w’（保证这条边在 edges 中存在）；

• [2, x]：询问从根节点 1 到节点 x 的最短路径长度（按当前边权计算）。

要求返回一个整数数组 answer，按操作顺序记录每个类型为 [2, x] 的查询结果。注意边权的修改会影响后续的查询结果。

1 <= n <= 100000。

edges.length == n - 1。

edges[i] == [ui, vi, wi]。

1 <= ui, vi <= n。

1 <= wi <= 10000。

输入保证 edges 构成一棵合法的树。

1 <= queries.length == q <= 100000。

queries[i].length == 2 或 4。

queries[i] == [1, u, v, w’]，或者queries[i] == [2, x]。

1 <= u, v, x <= n。

(u, v) 一定是 edges 中的一条边。

1 <= w’ <= 10000。

输入： n = 3, edges = [[1,2,2],[1,3,4]], queries = [[2,1],[2,3],[1,1,3,7],[2,2],[2,3]]。

输出： [0,4,2,7]。

解释：

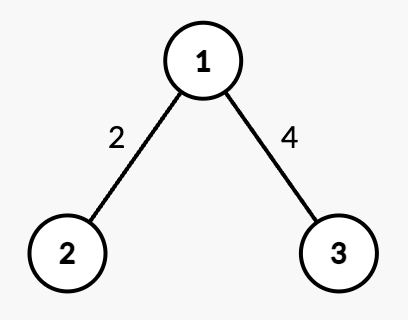
查询 [2,1]：从根节点 1 到节点 1 的最短路径为 0。

查询 [2,3]：从根节点 1 到节点 3 的最短路径为 4。

操作 [1,1,3,7]：边 (1,3) 的权重从 4 改为 7。

查询 [2,2]：从根节点 1 到节点 2 的最短路径为 2。

查询 [2,3]：从根节点 1 到节点 3 的最短路径为 7。

题目来自力扣3515。

解决方案步骤

1. 构建树结构

• 使用邻接表 g 存储树结构
• 每个节点存储其相邻节点列表

2. DFS遍历进行欧拉序编号

• 从根节点1开始进行深度优先搜索(DFS)
• 为每个节点分配进入时间 in[x] 和离开时间 out[x]
• 这种编号方式使得以节点x为根的子树在区间 [in[x], out[x]] 内
• 时间戳从1开始递增

3. 建立边权与节点的映射

• 对于每条边 (u, v)，将边权存储在子节点的 weight 数组中
• 具体来说：如果v是u的子节点，则边权存储在 weight[v] 中
• 通过DFS时的父子关系确定谁是子节点

4. 使用树状数组维护路径和

• 创建大小为n+1的树状数组 diff
• 关键思想：从根节点1到节点x的路径和 = diff.pre(in[x])
• 当修改边权时，只更新以该边子节点为根的子树中的所有节点

5. 处理操作

对于修改操作 [1, u, v, w']：

• 确定哪个节点是子节点（通过比较 in 时间戳）
• 计算边权的增量：d = 新权值 - 旧权值
• 更新 weight 数组
• 在树状数组中进行区间更新：将子树中所有节点的值增加 d
  • diff.update(in[y], d) 在子树的开始位置增加
  • diff.update(out[y]+1, -d) 在子树结束的下一个位置减少
  • 这样只有子树内的节点在查询前缀和时会包含这个增量

对于查询操作 [2, x]：

• 直接返回 diff.pre(in[x])
• 因为树状数组的前缀和正好对应从根到节点x的路径和

示例执行过程

以题目中的例子说明：

• 初始边权：(1,2)=2, (1,3)=4
• DFS后：节点1的子树包含所有节点
• 初始时，从1到3的路径和为4
• 修改边 (1,3) 权值为7后，子树3中的所有节点（只有节点3）路径和增加3
• 查询节点3时得到7

复杂度分析

时间复杂度

• DFS遍历：O(n)，每个节点访问一次
• 每次修改操作：O(log n)，树状数组的更新操作
• 每次查询操作：O(log n)，树状数组的查询操作
• 总体：O(n + q log n)，其中n是节点数，q是操作数

空间复杂度

• 邻接表：O(n)
• in/out数组：O(n)
• weight数组：O(n)
• 树状数组：O(n)
• 总体：O(n)

这种方法利用了树的DFS序和树状数组的高效区间更新/单点查询特性，能够高效处理大规模的边权修改和路径查询。

Go完整代码如下：

package main

import (
	"fmt"
)

type fenwick []int

func newFenwickTree(n int) fenwick {
	return make(fenwick, n+1) // 使用下标 1 到 n
}

// a[i] 增加 val
// 1 <= i <= n
func (f fenwick) update(i, val int) {
	for ; i < len(f); i += i & -i {
		f[i] += val
	}
}

// 求前缀和 a[1] + ... + a[i]
// 1 <= i <= n
func (f fenwick) pre(i int) (s int) {
	for ; i > 0; i &= i - 1 {
		s += f[i]
	}
	return
}

func treeQueries(n int, edges [][]int, queries [][]int) (ans []int) {
	g := make([][]int, n+1)
	for _, e := range edges {
		x, y := e[0], e[1]
		g[x] = append(g[x], y)
		g[y] = append(g[y], x)
	}

	in := make([]int, n+1)
	out := make([]int, n+1)
	clock := 0
	var dfs func(int, int)
	dfs = func(x, fa int) {
		clock++
		in[x] = clock // 进来的时间
		for _, y := range g[x] {
			if y != fa {
				dfs(y, x)
			}
		}
		out[x] = clock // 离开的时间
	}
	dfs(1, 0)

	// 对于一条边 x-y（y 是 x 的儿子），把边权保存在 weight[y] 中
	weight := make([]int, n+1)
	diff := newFenwickTree(n)
	update := func(x, y, w int) {
		// 保证 y 是 x 的儿子
		if in[x] > in[y] {
			y = x
		}
		d := w - weight[y] // 边权的增量
		weight[y] = w
		// 把子树 y 中的最短路长度都增加 d（用差分树状数组维护）
		diff.update(in[y], d)
		diff.update(out[y]+1, -d)
	}

	for _, e := range edges {
		update(e[0], e[1], e[2])
	}

	for _, q := range queries {
		if q[0] == 1 {
			update(q[1], q[2], q[3])
		} else {
			ans = append(ans, diff.pre(in[q[1]]))
		}
	}
	return
}

func main() {
	n := 3
	edges := [][]int{{1, 2, 2}, {1, 3, 4}}
	queries := [][]int{{2, 1}, {2, 3}, {1, 1, 3, 7}, {2, 2}, {2, 3}}
	result := treeQueries(n, edges, queries)
	fmt.Println(result)
}

Python完整代码如下：

# -*-coding:utf-8-*-

class Fenwick:
    def __init__(self, n):
        self.n = n
        self.tree = [0] * (n + 1)  # Using indices 1 to n
    
    def update(self, i, val):
        while i < len(self.tree):
            self.tree[i] += val
            i += i & -i
    
    def pre(self, i):
        s = 0
        while i > 0:
            s += self.tree[i]
            i &= i - 1
        return s

def tree_queries(n, edges, queries):
    g = [[] for _ in range(n + 1)]
    for e in edges:
        x, y = e[0], e[1]
        g[x].append(y)
        g[y].append(x)
    
    in_time = [0] * (n + 1)
    out_time = [0] * (n + 1)
    clock = 0
    
    def dfs(x, fa):
        nonlocal clock
        clock += 1
        in_time[x] = clock  # Entry time
        for y in g[x]:
            if y != fa:
                dfs(y, x)
        out_time[x] = clock  # Exit time
    
    dfs(1, 0)
    
    # For an edge x-y (where y is x's child), store the edge weight in weight[y]
    weight = [0] * (n + 1)
    diff = Fenwick(n)
    
    def update_edge(x, y, w):
        # Ensure y is x's child
        if in_time[x] > in_time[y]:
            y = x
        d = w - weight[y]  # Increment in edge weight
        weight[y] = w
        # Increase the shortest path length in subtree y by d (using Fenwick tree)
        diff.update(in_time[y], d)
        diff.update(out_time[y] + 1, -d)
    
    for e in edges:
        update_edge(e[0], e[1], e[2])
    
    ans = []
    for q in queries:
        if q[0] == 1:
            update_edge(q[1], q[2], q[3])
        else:
            ans.append(diff.pre(in_time[q[1]]))
    return ans

def main():
    n = 3
    edges = [[1, 2, 2], [1, 3, 4]]
    queries = [[2, 1], [2, 3], [1, 1, 3, 7], [2, 2], [2, 3]]
    result = tree_queries(n, edges, queries)
    print(result)

if __name__ == "__main__":
    main()