堆(Heap or PriorityQueue) Java

认识堆（优先级队列）

1.堆又叫优先级队列，逻辑上上是一棵完全二叉树，堆物理上基于数组实现
2.堆可分为大堆（大根堆、最大堆）和小堆（小根堆、最小堆）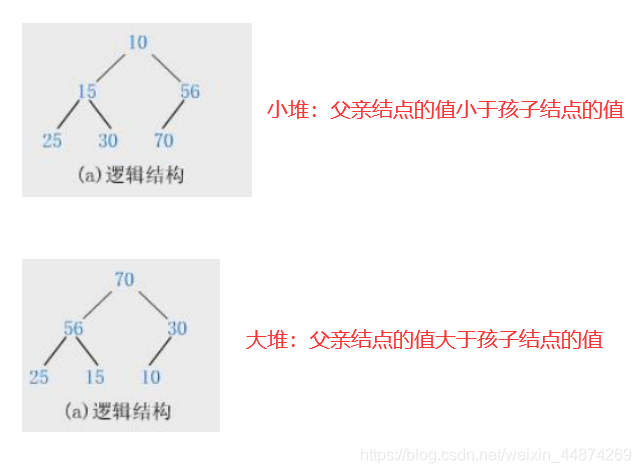

堆（优先级队列）操作方法

public class MyHeap {

    private int[] elem;
    private int usedSzie;

    public MyHeap(int k){
        this.elem = new int[k];
    }

    //创建大堆
    public void createBigHeap(int[] arr){
        for (int i = 0; i < arr.length; i++) {
            this.elem[i] = arr[i];
            this.usedSzie++;
        }
        //i表示父亲结点，依次调整
        for (int i = (this.usedSzie-2)/2; i >= 0 ; i--) {
            adjustDown(i, this.usedSzie);
        }
    }

    //向下调整
    public void adjustDown(int parent, int len){
        int child = 2*parent+1;
        //len代表数组实际长度
        //child小于len说明 parent有左孩子，不能确定是否有右孩子 child==len说明 parent没有左右孩子
        while(child < len){
            //child+1 < len保证当前父亲结点有右孩子
            //当左孩子小于右孩子时，child走到右孩子下标，保证child是左右孩子最大值下标
            if(child+1 < len &&this.elem[child] < this.elem[child+1]){
                child++;
            }
            //当孩子结点大于父亲结点时，交换
            if(this.elem[child] > this.elem[parent]){
                int tmp = this.elem[child];
                this.elem[child] = this.elem[parent];
                this.elem[parent] = tmp;
                parent = child;
                child = 2*parent+1;
            }else{
                //我们是从最后一棵树调整的
                //当this.elem[child] <= this.elem[parent]时,表明此时的树是大根堆，后面不需要循环了
                break;
            }
        }
    }

    //创建小堆
    public void createSmallHeap(int[] arr){
        for (int i = 0; i < arr.length; i++) {
            this.elem[i] = arr[i];
            this.usedSzie++;
        }
        //i表示父亲结点，依次调整
        for (int i = (this.usedSzie-2)/2; i >= 0 ; i--) {
            adjustDown1(i, this.usedSzie);
        }
    }

    //向下调整
    public void adjustDown1(int parent, int len){
        int child = 2*parent+1;
        //len代表数组实际长度
        //child小于len说明 parent有左孩子，不能确定是否有右孩子 child==len说明 parent没有左右孩子
        while(child < len){
            //child+1 < len保证当前父亲结点有右孩子
            //当左孩子小于右孩子时，child走到右孩子下标，保证child是左右孩子最大值下标
            if(child+1 < len &&this.elem[child] > this.elem[child+1]){
                child++;
            }
            //当孩子结点大于父亲结点时，交换
            if(this.elem[child] < this.elem[parent]){
                int tmp = this.elem[child];
                this.elem[child] = this.elem[parent];
                this.elem[parent] = tmp;
                parent = child;
                child = 2*parent+1;
            }else{
                //我们是从最后一棵树调整的
                //当this.elem[?child] <= this.elem[parent]时,表明此时的树是大根堆，后面不需要循环了
                break;
            }
        }
    }


    //向上调整
    //这里的child第一次就是入队元素的下标，
    public void adjustUp(int child){
        int parent = (child-1)/2;
        //child等于0相当于已经调整了位置，此时parent为负数了
        while(child > 0){
            if(this.elem[child] > this.elem[parent]){
                int tmp = this.elem[child];
                this.elem[child] = this.elem[parent];
                this.elem[parent] = tmp;
                child = parent;
                parent = (child-1)/2;
            }else{
                break;
            }
        }
    }

    //元素入优先级队列
    //逻辑：将元素放在数组最后位置，然后堆向上调整
    public void push(int val){
        if(isFull()){
            this.elem = Arrays.copyOf(this.elem, this.elem.length*2);
        }
        this.elem[usedSzie] = val;
        this.usedSzie++; //例如元素为10，此时useDsize为11
        adjustUp(usedSzie-1);
    }

    //元素出优先级队列
    //思想：队头和队尾交换 向下调整0下标这棵树
    public int poll(){
        if(isEmpty()) {
            throw new RuntimeException("队列为空");
        }
        int ret = this.elem[0]; //保存队头元素
        int tmp = this.elem[0];
        this.elem[0] = this.elem[usedSzie];
        this.elem[usedSzie] = tmp;
        //相当于原来的队头元素被拿走了
        this.usedSzie--;  /
        adjustDown(0,usedSzie);
        return ret;
    }

    //拿到队头元素不删除
    public int peek(){
        if(isEmpty()) {
            throw new RuntimeException("队列为空");
        }
        return this.elem[0];
    }


    //优先级队列用堆创建，而堆基于数组，当数组已满时，需要扩容
    public boolean isFull(){
        return this.usedSzie == this.elem.length;
    }

    //判空
    public boolean isEmpty(){
        return this.usedSzie == 0;
    }

    public void display(){
        for (int i = 0; i < this.usedSzie; i++) {
            if(i == 0) {
                System.out.print("["+this.elem[i]+" ");
            }else if(i == usedSzie-1){
                System.out.print(this.elem[i]+"]");
            }else{
                System.out.print(this.elem[i]+" ");
            }
        }
    }


}

主函数测试用例

public class TestDemo {
    public static void main(String[] args) {
        MyHeap heap = new MyHeap(10);
        int[] array = {27,15,19,18,28,34,65,49,25,37};
        System.out.println("原来的堆: "+Arrays.toString(array));
        heap.createBigHeap(array);
        System.out.print("现在的大根堆: ");
        heap.display();
        System.out.println();
        heap.push(200);
        heap.display();
        System.out.println(heap.poll());
        heap.display();
    }
}