2025-11-05：网格传送门旅游。用go语言，给定一个大小为 m x n 的字符网格 matrix（用字符串数组表示），其中每个格子可能是三类之一：

• ‘.’ 表示可通行的空格；

• ‘#’ 表示不可经过的障碍；

• 大写字母 ‘A’ 到 ‘Z’ 表示传送门。

起点是左上角 (0,0)，终点是右下角 (m-1,n-1)。每一步可以向上下左右相邻格子移动，前提是目标格在边界内且不是障碍。若走到一个字母格，并且此前还没有使用过该字母对应的传送门，你可以选择立刻瞬移到网格中另一个具有相同字母的格子（这次瞬移不消耗步数）。每个字母的传送功能在整趟路径中最多只能使用一次。

要求计算到达终点所需的最少移动步数；若无法抵达则返回 -1。

1 <= m == matrix.length <= 1000。

1 <= n == matrix[i].length <= 1000。

matrix[i][j] 是 ‘#’、‘.’ 或一个大写英文字母。

matrix[0][0] 不是障碍物。

输入： matrix = [“A…”,“.A.”,“…”]。

输出： 2。

解释：

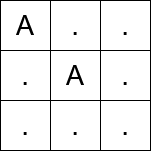
在第一次移动之前，从 (0, 0) 传送到 (1, 1)。

第一次移动，从 (1, 1) 移动到 (1, 2)。

第二次移动，从 (1, 2) 移动到 (2, 2)。

题目来自力扣3552。

分步骤详细过程

1. 初始化与数据预处理

   • 获取网格的行数 m 和列数 n，检查终点 (m-1, n-1) 是否为障碍物 #，若是则直接返回 -1。
   • 创建一个映射 pos（数组长度为 'Z'+1），用于记录每个大写字母（传送门）在网格中的所有位置。遍历网格，将每个字母的坐标存入对应字母的列表中。例如，字母 A 的所有位置会存储在 pos['A'] 中。
   • 初始化一个距离矩阵 dis，尺寸与网格相同，所有值设为极大值（math.MaxInt），表示初始时所有位置不可达。起点 (0,0) 的距离设为 0。
   • 定义四个移动方向：上下左右（dirs）。

2. 双向队列 BFS（0-1 BFS）

   • 使用两个队列 q0 和 q1 模拟双端队列（deque）。q0 存储当前步数不增加的节点（如通过传送门移动），q1 存储步数增加 1 的节点（如向相邻格子移动）。初始时将起点 (0,0) 加入 q0。
   • 循环处理队列，优先从 q0 弹出节点（保证步数最小的先被处理），若 q0 为空则从 q1 头部弹出节点。
   • 对于当前节点 p：
     • 若 p 是终点，直接返回其距离 d。
     • 传送门处理：若 p 是大写字母（即传送门），且该字母的传送功能未被使用过（pos[c] 非空），则遍历该字母的所有其他传送门位置：
       • 若目标位置的距离大于当前距离 d，则更新其距离为 d（传送不消耗步数），并将该位置加入 q0 队首（因为步数未增加，需优先处理）。
       • 处理完成后，清空该字母的传送门列表 pos[c] = nil，避免重复使用。
     • 普通移动：遍历上下左右四个方向，计算相邻格子坐标 (x, y)。若新坐标合法、非障碍物且新距离 d+1 小于当前记录的距离，则更新距离并将新坐标加入 q1 队尾（步数增加 1）。

3. 终止条件

   • 若终点被访问到，返回其最短距离。
   • 若所有队列处理完毕仍未到达终点，返回 -1。

时间与空间复杂度

• 时间复杂度：O(m × n)。
  每个网格节点最多被处理一次，且每次处理包括检查传送门（每个字母最多触发一次）和四个方向的移动（常数时间）。使用双端队列后，BFS 的摊还时间复杂度为线性。
• 空间复杂度：O(m × n)。
  主要用于存储距离矩阵 dis（m × n）、传送门位置映射 pos（最多 26 个字母，每个字母的位置列表总大小不超过 m × n），以及队列空间（最多存储 m × n 个节点）。

关键点说明

• 双端队列优化：将不增加步数的传送门移动（权重 0）加入队首，普通移动（权重 1）加入队尾，保证 BFS 始终优先处理步数更少的节点，无需显式排序。
• 传送门去重：通过清空 pos[c] 确保每个字母的传送功能仅使用一次，避免无限循环。
• 示例中，从 (0,0)（字母 A）传送到 (1,1)（另一个 A）后，步数仍为 0，随后移动两次到达终点，总步数为 2。

Go完整代码如下：

package main

import (
	"fmt"
	"math"
	"unicode"
)

func minMoves(matrix []string) int {
	m, n := len(matrix), len(matrix[0])
	if matrix[m-1][n-1] == '#' {
		return -1
	}

	type pair struct{ x, y int }
	pos := ['Z' + 1][]pair{}
	for i, row := range matrix {
		for j, c := range row {
			if unicode.IsUpper(c) {
				pos[c] = append(pos[c], pair{i, j})
			}
		}
	}

	dirs := []pair{{0, -1}, {0, 1}, {-1, 0}, {1, 0}}
	dis := make([][]int, m)
	for i := range dis {
		dis[i] = make([]int, n)
		for j := range dis[i] {
			dis[i][j] = math.MaxInt
		}
	}
	dis[0][0] = 0

	// 两个 slice 头对头，模拟 deque
	q0 := []pair{{}}
	q1 := []pair{}

	for len(q0) > 0 || len(q1) > 0 {
		// 弹出队首
		var p pair
		if len(q0) > 0 {
			p, q0 = q0[len(q0)-1], q0[:len(q0)-1]
		} else {
			p, q1 = q1[0], q1[1:]
		}
		d := dis[p.x][p.y]

		if p.x == m-1 && p.y == n-1 {
			return d
		}

		if c := matrix[p.x][p.y]; c != '.' {
			// 使用所有传送门
			for _, q := range pos[c] {
				x, y := q.x, q.y
				if d < dis[x][y] {
					dis[x][y] = d
					q0 = append(q0, pair{x, y}) // 加到队首
				}
			}
			pos[c] = nil // 避免重复使用传送门
		}

		// 下面代码和普通 BFS 是一样的
		for _, dir := range dirs {
			x, y := p.x+dir.x, p.y+dir.y
			if 0 <= x && x < m && 0 <= y && y < n && matrix[x][y] != '#' && d+1 < dis[x][y] {
				dis[x][y] = d + 1
				q1 = append(q1, pair{x, y}) // 加到队尾
			}
		}
	}

	return -1
}

func main() {
	matrix := []string{"A..", ".A.", "..."}
	result := minMoves(matrix)
	fmt.Println(result)
}

Python完整代码如下：

# -*-coding:utf-8-*-

import math
from collections import deque

def minMoves(matrix):
    m, n = len(matrix), len(matrix[0])
    if matrix[m-1][n-1] == '#':
        return -1

    # 预处理所有传送门的位置
    pos = {}
    for i in range(m):
        for j in range(n):
            c = matrix[i][j]
            if c.isupper():
                if c not in pos:
                    pos[c] = []
                pos[c].append((i, j))

    dirs = [(0, -1), (0, 1), (-1, 0), (1, 0)]
    
    # 初始化距离矩阵
    dis = [[math.inf] * n for _ in range(m)]
    dis[0][0] = 0

    # 使用两个deque模拟双端队列
    q0 = deque([(0, 0)])
    q1 = deque()

    while q0 or q1:
        # 弹出队首元素
        if q0:
            x, y = q0.pop()
        else:
            x, y = q1.popleft()
        
        d = dis[x][y]
        
        # 到达终点
        if x == m-1 and y == n-1:
            return d
        
        # 如果是传送门，处理所有相同字母的位置
        c = matrix[x][y]
        if c != '.' and c in pos:
            for nx, ny in pos[c]:
                if d < dis[nx][ny]:
                    dis[nx][ny] = d
                    q0.append((nx, ny))  # 加到队首
            # 使用后删除该传送门，避免重复使用
            del pos[c]
        
        # 处理四个方向的移动
        for dx, dy in dirs:
            nx, ny = x + dx, y + dy
            if 0 <= nx < m and 0 <= ny < n and matrix[nx][ny] != '#' and d + 1 < dis[nx][ny]:
                dis[nx][ny] = d + 1
                q1.append((nx, ny))  # 加到队尾
                
    return -1

def main():
    matrix = ["A..", ".A.", "..."]
    result = minMoves(matrix)
    print(result)

if __name__ == "__main__":
    main()