1.树的定义

树是n（n>=0）个结点的有限集合T，当n=0时，称为空树，当n>0时，该集合满足如下条件：
1.其中必有一个称为根的特定结点，它没有直接前驱，但是有零个或多个直接后续。
2.其中n-1个结点可以划分成m（m>=0）个互不相交的有限集T1，T2，T3，T4…其中Ti又是一棵树，称为根的子树，每棵子树的根结点有且仅有一个直接前驱，但有零个或者多个直接后续。

2.树的基本术语

除了以上术语，也常常借助人类家族树来表示，以便于直观理解结点之间层次关系，你一定记得高中生物的家谱图。

文本形式：
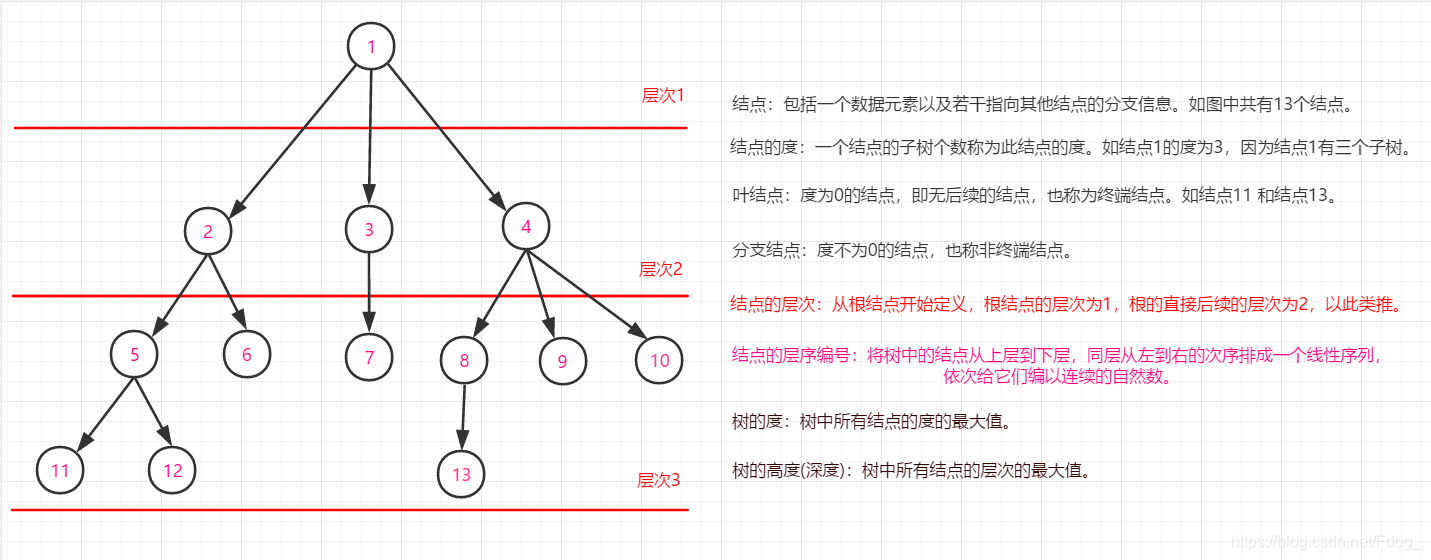
1.结点：包括一个数据元素以及若干指向其他结点的分支信息。

2.结点的度：一个结点的子树个数称为此结点的度。

3.叶结点：度为0的结点，即无后续的结点，也称为终端结点。

4.分支结点：度不为0的结点，也称非终端结点。

5.结点的层次：从根结点开始定义，根结点的层次为1，根的直接后续的层次为2，以此类推。

6.结点的层序编号：将树中的结点从上层到下层，同层从左到右的次序排成一个线性序列，依次给它们编以连续的自然数。

7.树的度：树中所有结点的度的最大值。

8.树的高度(深度)：树中所有结点的层次的最大值。

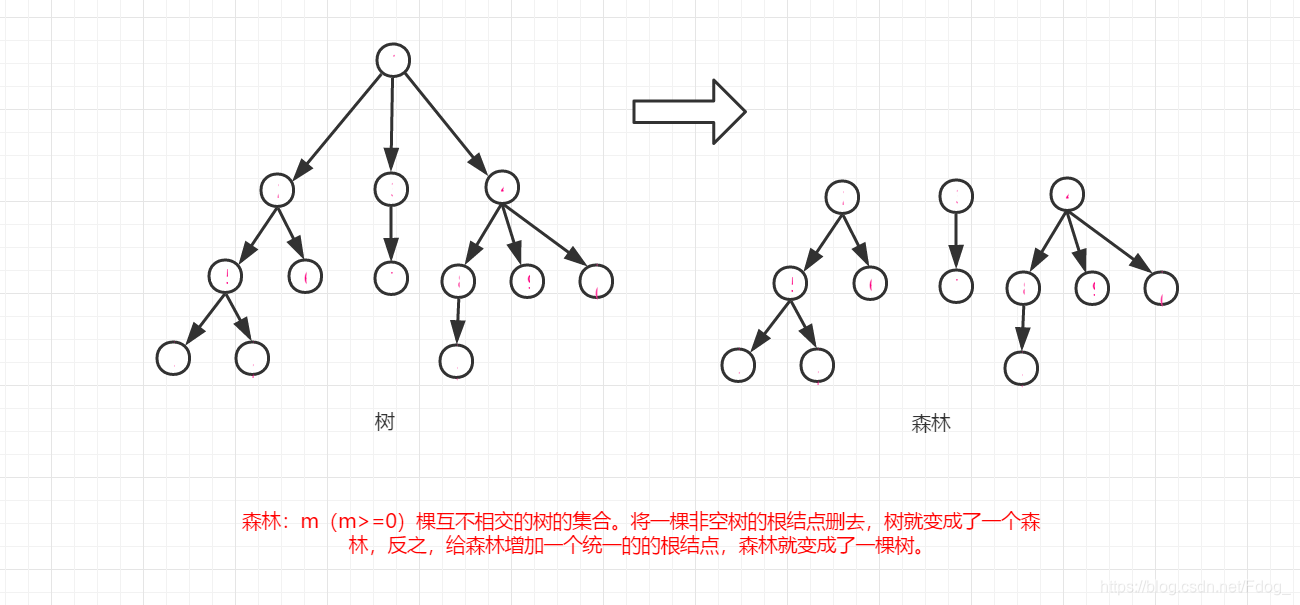
9.森林：m（m>=0）棵互不相交的树的集合。将一棵非空树的根结点删去，树就变成了一个森林，反之，给森林增加一个统一的的根结点，森林就变成了一棵树。

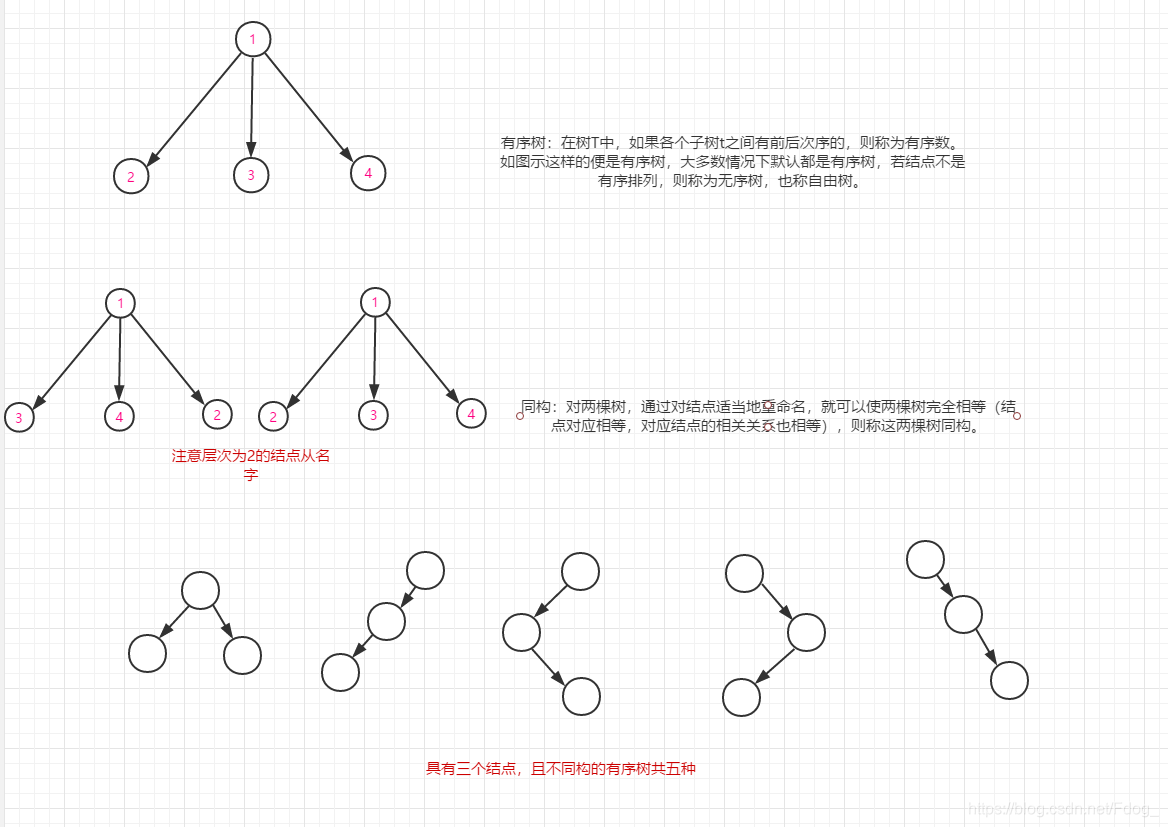
10.有序树：在树T中，如果各个子树t之间有前后次序的，则称为有序数。
如图示这样的便是有序树，大多数情况下默认都是有序树，若结点不是有序排列，则称为无序树，也称自由树。

11.同构：对两棵树，通过对结点适当地重命名，就可以使两棵树完全相等（结点对应相等，对应结点的相关关系也相等），则称这两棵树同构。

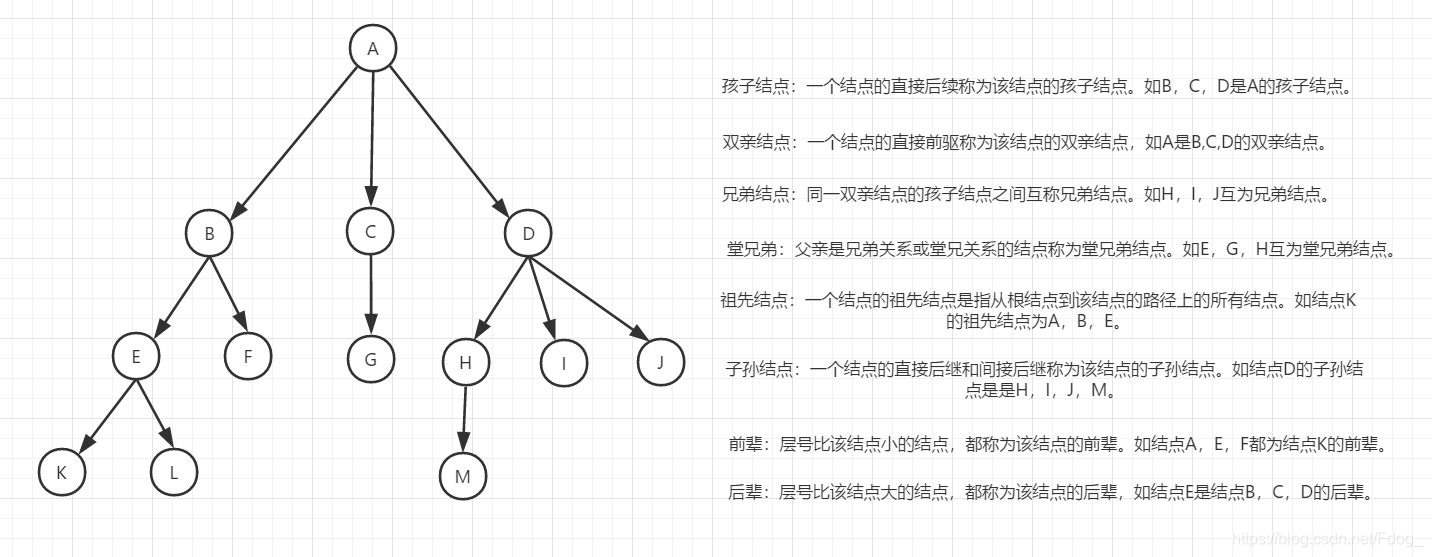
12.孩子结点：一个结点的直接后续称为该结点的孩子结点。

13.双亲结点：一个结点的直接前驱称为该结点的双亲结点。

14.兄弟结点：同一双亲结点的孩子结点之间互称兄弟结点。

15.堂兄弟：父亲是兄弟关系或堂兄关系的结点称为堂兄弟结点。

16.祖先结点：一个结点的祖先结点是指从根结点到该结点的路径上的所有结点。

17.子孙结点：一个结点的直接后继和间接后继称为该结点的子孙结点。

18.前辈：层号比该结点小的结点，都称为该结点的前辈。

19.后辈：层号比该结点大的结点，都称为该结点的后辈。

若有错误，欢迎指正批评，欢迎评论。
每文一句：线别忘了答应自己要做的事情，也别忘了答应自己要去的地方，无论那有多难，有多远。

文章来源: blog.csdn.net，作者：花狗Fdog，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/Fdog_/article/details/104746976